题目内容
【题目】已知椭圆
的左、右顶点分别为
，
，上下顶点分别为
，
，左、右焦点分别为
，
，离心率为e.
（1）若
，设四边形
的面积为
，四边形
的面积为
，且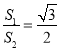
，求椭圆C的方程；
（2）若
，设直线
与椭圆C相交于P，Q两点，
分别为线段
，
的中点，坐标原点O在以MN为直径的圆上，且
，求实数k的取值范围.
【答案】（1）
（2）
【解析】
（1）依题意可得，
，
，再结合
，即可解出
，得出椭圆C的方程；
（2）联立直线和椭圆C的方程，可解得
，
，再利用坐标原点O在以MN为直径的圆上，得到
，且
为矩形，因此
，即可用
表示出
，然后根据离心率的范围求出的范围，即可根据二次函数的知识求出．
（1）
，∴，由
，可得
，化为，
联立
，解得
，
，
，∴椭圆C的方程为.
（2）设
，
，联立
，可得
，
∴，.
由题意可知：，且为矩形，
∴
，而
，
∴
，
即
，∴
，
∵
，∴
，
可得
，∴
.
练习册系列答案
相关题目
