题目内容
若r(x):sinx+cosx>m,s(x):x2+mx+1>0,如果对于?x∈R,r(x)为假命题且s(x)为真命题,则实数m的取值范围是 .
考点:复合命题的真假
专题:简易逻辑
分析:先求出命题r(x)与s(x)成立的等价条件,利用r(x)为假命题且s(x)为真命题.确定实数m的取值范围.
解答:
解:∵sinx+cosx=
sin(x+
)≥-
,
∴要使sinx+cosx>m恒成立,则m<-
,
即:r(x):m<-
.
若x2+mx+1>0成立,则△=m2-4<0,
解得-2<m<2,
即s(x):-2<m<2.
∵r(x)为假命题,∴m≥-
∵s(x)为真命题,则
,解得-
≤m<2.
综上-
≤m<2.
故答案为:{m|-
≤m<2}.
| 2 |
| π |
| 4 |
| 2 |
∴要使sinx+cosx>m恒成立,则m<-
| 2 |
即:r(x):m<-
| 2 |
若x2+mx+1>0成立,则△=m2-4<0,
解得-2<m<2,
即s(x):-2<m<2.
∵r(x)为假命题,∴m≥-
| 2 |
∵s(x)为真命题,则
|
| 2 |
综上-
| 2 |
故答案为:{m|-
| 2 |
点评:本题主要考查复合命题与简单命题之间的关系,利用函数的性质求出命题成立的等价条件是解决的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
在计算数列{2-n}前100项和的程序框图中,框内空白处应填入的计算语句是( )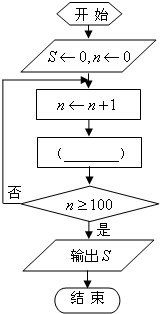

| A、S←2-1+2-2+…+2-n |
| B、S←S+2-n |
| C、S←2-1+2-2+…+2-100 |
| D、S←S+2-n-1 |
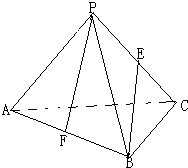 如图,在正四面体PABC中,若E,F分别是PC,AB的中点,则异面直线PF与BE所成的角的余弦值为
如图,在正四面体PABC中,若E,F分别是PC,AB的中点,则异面直线PF与BE所成的角的余弦值为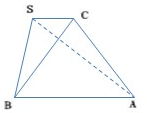 已知在三棱锥S-ABC中,△SBC、△ABC都是等边三角形,平面SBC⊥平面ABC,SA=6,则三棱锥体积为
已知在三棱锥S-ABC中,△SBC、△ABC都是等边三角形,平面SBC⊥平面ABC,SA=6,则三棱锥体积为