题目内容
已知双曲线C: (a>0,b>0)的右准线与一条渐近线交于点M,F是右焦点,若|MF|=1,且双曲线C的离心率
(a>0,b>0)的右准线与一条渐近线交于点M,F是右焦点,若|MF|=1,且双曲线C的离心率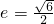 .
.
(1)求双曲线C的方程;
(2)过点A(0,1)的直线l与双曲线C的右支交于不同两点P、Q,且P在A、Q之间,若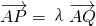 且
且 ,求直线l斜率k的取值范围.
,求直线l斜率k的取值范围.
解:(1)由对称性,不妨设M是右准线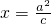 与一渐近线
与一渐近线 的交点,
的交点,
其坐标为M( ),∵|MF|=1,∴
),∵|MF|=1,∴ ,
,
又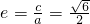 ∴
∴ ,
,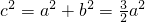 ,
,
解得a2=2,b2=1,所以双曲线C的方程是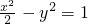 ;(6分)
;(6分)
(2)设直线l的斜率为k,则l的方程为y=kx+1,设点P(x1,y1),Q(x2,y2),
由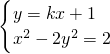 得:(1-2k2)x2-4kx-4=0,
得:(1-2k2)x2-4kx-4=0,
∵l与双曲线C的右支交于不同的两点P、Q,
∴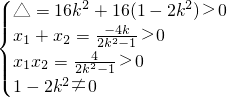
∴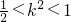 且k<0①(9分)
且k<0①(9分)
又∵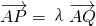 且P在A、Q之间,
且P在A、Q之间, ,∴x1=λx2且
,∴x1=λx2且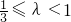 ,
,
∴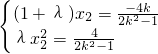 ∴
∴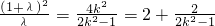 ,
,
∵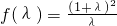 =
=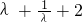 在
在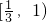 上是减函数(∵f′(λ)<0),
上是减函数(∵f′(λ)<0),
∴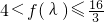 ,
,
∴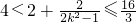 ,由于
,由于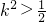 ,∴
,∴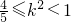 ②(12分)
②(12分)
由①②可得: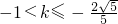 ,(13分)
,(13分)
即直线l斜率取值范围为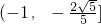 (14分)
(14分)
分析:(1)利用双曲线的右准线与一条渐近线交于点M,可求点M的坐标,由|MF|=1,可得方程,借助于离心率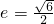 及几何量的关系,从而求出双曲线的方程;
及几何量的关系,从而求出双曲线的方程;
(2)将直线与双曲线的方程联立可得(1-2k2)x2-4kx-4=0,,从而可有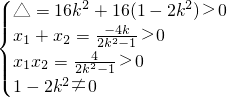 ,即
,即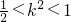 且k<0,再根据
且k<0,再根据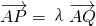 且
且 ,有
,有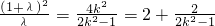 ,从而可求k的取值范围.
,从而可求k的取值范围.
点评:本题考查双曲线标准方程的求解,关键是寻找几何量之间的关系,考查直线与双曲线的位置关系,通过联立方程组,借助于根与系数的关系,从而使问题得解.
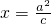 与一渐近线
与一渐近线 的交点,
的交点,其坐标为M(
 ),∵|MF|=1,∴
),∵|MF|=1,∴ ,
,又
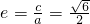 ∴
∴ ,
,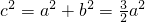 ,
,解得a2=2,b2=1,所以双曲线C的方程是
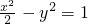 ;(6分)
;(6分)(2)设直线l的斜率为k,则l的方程为y=kx+1,设点P(x1,y1),Q(x2,y2),
由
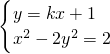 得:(1-2k2)x2-4kx-4=0,
得:(1-2k2)x2-4kx-4=0,∵l与双曲线C的右支交于不同的两点P、Q,
∴
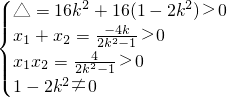
∴
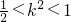 且k<0①(9分)
且k<0①(9分)又∵
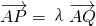 且P在A、Q之间,
且P在A、Q之间, ,∴x1=λx2且
,∴x1=λx2且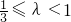 ,
,∴
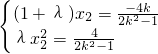 ∴
∴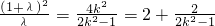 ,
,∵
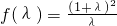 =
=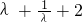 在
在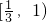 上是减函数(∵f′(λ)<0),
上是减函数(∵f′(λ)<0),∴
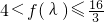 ,
,∴
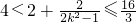 ,由于
,由于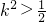 ,∴
,∴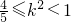 ②(12分)
②(12分)由①②可得:
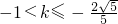 ,(13分)
,(13分)即直线l斜率取值范围为
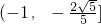 (14分)
(14分)分析:(1)利用双曲线的右准线与一条渐近线交于点M,可求点M的坐标,由|MF|=1,可得方程,借助于离心率
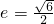 及几何量的关系,从而求出双曲线的方程;
及几何量的关系,从而求出双曲线的方程;(2)将直线与双曲线的方程联立可得(1-2k2)x2-4kx-4=0,,从而可有
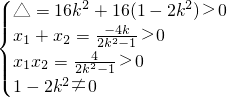 ,即
,即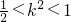 且k<0,再根据
且k<0,再根据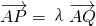 且
且 ,有
,有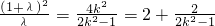 ,从而可求k的取值范围.
,从而可求k的取值范围.点评:本题考查双曲线标准方程的求解,关键是寻找几何量之间的关系,考查直线与双曲线的位置关系,通过联立方程组,借助于根与系数的关系,从而使问题得解.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目


 (a>0,b>0)的左、右焦点分别为
(a>0,b>0)的左、右焦点分别为 、
、 ,离心率为3,直线y=2与C的两个交点间的距离为
,离心率为3,直线y=2与C的两个交点间的距离为 .
. ,证明:
,证明: 、
、 、
、 成等比数列.
成等比数列. (a>0)的一条渐近线与直线l:2x-y+1=0垂直,则实数a= .
(a>0)的一条渐近线与直线l:2x-y+1=0垂直,则实数a= .