题目内容

已知椭圆E的方程是
x2
a2
+
y2
b2
=1（a＞b＞0），其左顶点为（-2，0），离心率e=
1
2
．
（1）求椭圆E的方程；
（2）已知倾斜角为45°且过右焦点的直线l交椭圆E于A、B两点，若椭圆上存在一点P，使
OP
=λ（
OA
+
OB
），试求λ的值．
（1）由已知得a=2，e=
c
a
=
1
2
，∴c=1，b=
a2-c2
=
3
，
∴椭圆E的方程为
x2
4
+
y2
3
=1．
（2）由（1）得右焦点F（1，0），因此直线l的方程为y=x-1．
代入椭圆方程并整理得7x2-8x-8=0．
设A（x1，y1），B（x2，y2），则x1+x2=
8
7
，
∴y1+y2=（x1-1）+（x2-1）=（x1+x2）-2=-
6
7
．
∴
OP
=λ（
OA
+
OB
）=λ（x1+x2，y1+y2）=λ（
8
7
，-
6
7
），
∴P点坐标为（
8λ
7
，-
6λ
7
），
代入椭圆方程，可得
(
8λ
7
)2
4
+
(-
6λ
7
)2
3
=1，
∴λ2=
7
4
，解得λ=±
7
2
．
练习册系列答案
相关题目
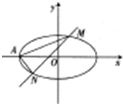精英家教网已知椭圆E的方程为：
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点坐标为（1，0），点P（1，
3
2
）在椭圆E上．
（I）求椭圆E的方程；
（II）过椭圆E的顶点A作两条互相垂直的直线分别与椭圆E交于（不同于点A的）两点M，N．
问：直线MN是否一定经过x轴上一定点？若是，求出定点坐标，不是，说明理由．
（2008•深圳一模）已知椭圆E的焦点在x轴上，长轴长为4，离心率为
3
2
．
（Ⅰ）求椭圆E的标准方程；
（Ⅱ）已知点A（0，1）和直线l：y=x+m，线段AB是椭圆E的一条弦且直线l垂直平分弦AB，求实数m的值．
已知椭圆E的中心是坐标原点，焦点在坐标轴上，且椭圆过点A（-2，0），B（2，0），C（1，
32
）三点．
（1）求椭圆E的方程；
（2）若点D为椭圆E上不同于A，B的任意一点，F（-1，0），H（1，0），当△DFH内切圆的面积最大时，求内切圆圆心的坐标；
（3）若直线l：y=k（x+4），（k≠0）与椭圆E交于M，N两点，点M关于x轴的对称点为P，试问直线PN能否过定点F（-1，0），若是，请证明；若不是，请说明理由．

如图，已知椭圆E的中心是原点O，其右焦点为F(2，0)，过x轴上一点A(3,0)作直线与椭圆E相交于P,Q两点,且的最大值为.

(Ⅰ)求椭圆E的方程;

(Ⅱ)设,过点P且平行于y轴的直线与椭圆E相交于另一点M,试问M,F,Q是否共线，若共线请证明；反之说明理由.

 
已知椭圆E的方程为：+=1（a＞b＞0）的右焦点坐标为（1，0），点P（1，）在椭圆E上．
（I）求椭圆E的方程；
（II）过椭圆E的顶点A作两条互相垂直的直线分别与椭圆E交于（不同于点A的）两点M，N．
问：直线MN是否一定经过x轴上一定点？若是，求出定点坐标，不是，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网