题目内容
如图,已知椭圆E的中心是原点O,其右焦点为F(2,0),过x轴上一点A(3,0)作直线 与椭圆E相交于P,Q两点,且
与椭圆E相交于P,Q两点,且 的最大值为
的最大值为 .
.

(Ⅰ)求椭圆E的方程;
(Ⅱ)设 ,过点P且平行于y轴的直线与椭圆E相交于另一点M,试问M,F,Q是否共线,若共线请证明;反之说明理由.
,过点P且平行于y轴的直线与椭圆E相交于另一点M,试问M,F,Q是否共线,若共线请证明;反之说明理由.
【答案】
(Ⅰ) 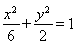 ; (Ⅱ)参考解析
; (Ⅱ)参考解析
【解析】
试题分析:(Ⅰ)因为右焦点为F(2,0),所以可得c=2,又因为过x轴上一点A(3,0)作直线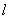 与椭圆E相交于P,Q两点,且
与椭圆E相交于P,Q两点,且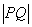 的最大值为
的最大值为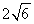 .所以
.所以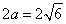 .再利用椭圆中
.再利用椭圆中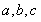 的关系式
的关系式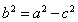 .即可求出b的值,从而可得结论.
.即可求出b的值,从而可得结论.
(Ⅱ)假设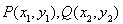 .通过
.通过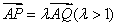 以及点在椭圆上,消去
以及点在椭圆上,消去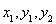 .即可得一个用
.即可得一个用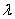 表示
表示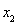 的一个等式.又由于
的一个等式.又由于 .通过对比向量
.通过对比向量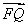 与
与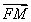 即可得结论.
即可得结论.
试题解析:(1)由题意可知: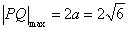 ,则
,则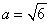 ,
,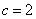 ,从而
,从而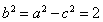 ,故所求椭圆
,故所求椭圆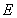 的方程为
的方程为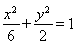 . 5分
. 5分
(2)解: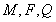 三点共线.
三点共线.
证明: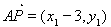 ,
, 由已知得方程组
由已知得方程组
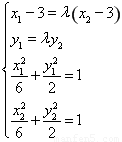 注意到
注意到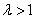 ,解得
,解得 ,因为
,因为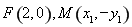 ,所以
,所以

 ,
,
又
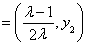 ,所以
,所以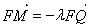 ,从而三点共线。 12分
,从而三点共线。 12分
考点:1.椭圆的基本性质.2.向量的共线问题.3.椭圆的标准方程.

练习册系列答案
相关题目
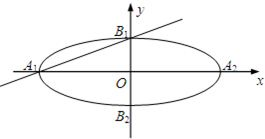
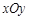 中,如图,已知椭圆E:
中,如图,已知椭圆E: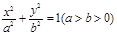 的左、右顶点分别为
的左、右顶点分别为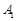 、
、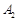 ,
,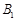 、
、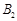 .设直线
.设直线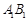 的倾斜角的正弦值为
的倾斜角的正弦值为 ,圆
,圆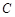 与以线段
与以线段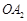 为直径的圆
为直径的圆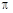 ,求圆
,求圆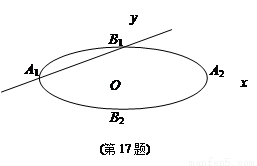
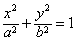 (a>b>0)的左、右顶点分别为A1,A2,上、下顶点分别为B1,B2。设直线A1B1的倾斜角的正弦值为
(a>b>0)的左、右顶点分别为A1,A2,上、下顶点分别为B1,B2。设直线A1B1的倾斜角的正弦值为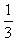 ,圆C与以线段OA2为直径的圆关于直线A1B1对称,
,圆C与以线段OA2为直径的圆关于直线A1B1对称,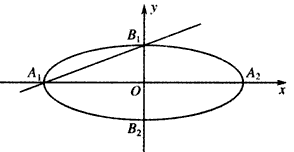
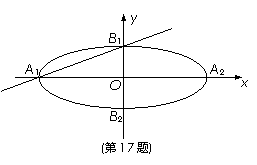
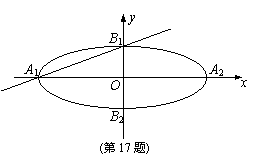 下顶点分别为
下顶点分别为