题目内容
 已知椭圆E的方程为:
已知椭圆E的方程为:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
(I)求椭圆E的方程;
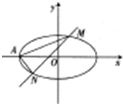
(II)过椭圆E的顶点A作两条互相垂直的直线分别与椭圆E交于(不同于点A的)两点M,N.
问:直线MN是否一定经过x轴上一定点?若是,求出定点坐标,不是,说明理由.
分析:(I)右焦点为(1,0),点P(1,
)在椭圆E上,2a=|PF1|+|PF2|=
+
=4,
由此能求出椭圆方程.
(II)设直线AM方程为y=k(x+2),由
,解得M(
,
),同理,得N(
,
),
若
=
,则得k2=1,即直线MN的方程为x= -
,此时过x轴上一点Q(-
,0),由此能导出直线MN过x轴上一定点Q(-
,0).
| 3 |
| 2 |
(1+1)2+(
|
(1-1) 2+(
|
由此能求出椭圆方程.
(II)设直线AM方程为y=k(x+2),由
|
| 6-8k2 |
| 3+4k2 |
| 12k |
| 3+4k2 |
| 6k2-8 |
| 3k2+4 |
| -12k |
| 3k2+4 |
若
| 6-8k2 |
| 3+4k2 |
| 6k2-8 |
| 3k2+4 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
| 7 |
解答:解:(I)∵右焦点为(1,0),∴c=1,左焦点为(-1,0),点P(1,
)在椭圆E上,
∴2a=|PF1|+|PF2|=
+
=4,
∴a=2,b=
,
∴椭圆方程为
+
=1.
(II)设直线AM方程为y=k(x+2),
则有
,整理,得(3+4k2)x2+16k2x+16k2-12=0,
解得M(
,
),同理,得N(
,
),
若
=
,则得k2=1,即直线MN的方程为
x= -
,此时过x轴上一点Q(-
,0)(10分)
当k2≠1时,假设直线MN过x轴上一定点Q(m,0),则有
∥
,
=(
-m,
),
=(m-
,
),则由
∥
,
解得m=-
,
所以直线MN过x轴上一定点Q(-
,0)(12分).
| 3 |
| 2 |
∴2a=|PF1|+|PF2|=
(1+1)2+(
|
(1-1) 2+(
|
∴a=2,b=
| 3 |
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(II)设直线AM方程为y=k(x+2),
则有
|
解得M(
| 6-8k2 |
| 3+4k2 |
| 12k |
| 3+4k2 |
| 6k2-8 |
| 3k2+4 |
| -12k |
| 3k2+4 |
若
| 6-8k2 |
| 3+4k2 |
| 6k2-8 |
| 3k2+4 |
x= -
| 2 |
| 7 |
| 2 |
| 7 |
当k2≠1时,假设直线MN过x轴上一定点Q(m,0),则有
| QM |
| NQ |
| QM |
| 6-8k2 |
| 3+4k2 |
| 12k |
| 3+4k2 |
| NQ |
| 6k2-8 |
| 3k2+4 |
| 12k |
| 3k2+4 |
| QM |
| NQ |
解得m=-
| 2 |
| 7 |
所以直线MN过x轴上一定点Q(-
| 2 |
| 7 |
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
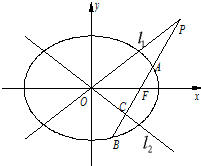 已知椭圆E的方程为
已知椭圆E的方程为 (2012•闵行区一模)已知椭圆E的方程为
(2012•闵行区一模)已知椭圆E的方程为