题目内容
(本小题满分14分)
已知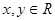 有
有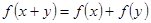
(1)判断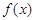 的奇偶性;
的奇偶性;
(2)若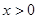 时,
时,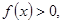 证明:
证明: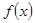 在
在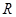 上为增函数;
上为增函数;
(3)在条件(2)下,若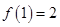 ,解不等式:
,解不等式: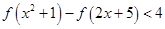
已知
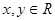 有
有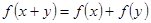
(1)判断
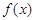 的奇偶性;
的奇偶性;(2)若
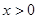 时,
时,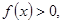 证明:
证明: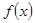 在
在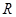 上为增函数;
上为增函数;(3)在条件(2)下,若
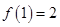 ,解不等式:
,解不等式: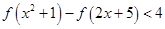
(1)奇函数;(2)见解析;(3) 。
。
 。
。(1)因为根据x,y取值的任意性,先令 得
得 ,又令
,又令 得
得
从而可得f(x)+f(-x)=f(x-x)=f(0)=0,所以f(-x)=-f(x),因此f(x)是R上的奇函数.
(2)设 ,则
,则 ,
, ,从而利用单调性的定义证出f(x)在R上是增函数.
,从而利用单调性的定义证出f(x)在R上是增函数.
(3)解此不等式第一个关键是确定f(1)+f(1)=f(2)=4,然后不等式 ,再利用f(x)在R上是增函数,脱掉法则符号f,转化为关于x的二次不等式求解即可.
,再利用f(x)在R上是增函数,脱掉法则符号f,转化为关于x的二次不等式求解即可.
解:1) 有
有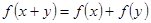
令 得
得 又令
又令 得
得
 即
即 解得
解得 …………14分
…………14分
 得
得 ,又令
,又令 得
得从而可得f(x)+f(-x)=f(x-x)=f(0)=0,所以f(-x)=-f(x),因此f(x)是R上的奇函数.
(2)设
 ,则
,则 ,
, ,从而利用单调性的定义证出f(x)在R上是增函数.
,从而利用单调性的定义证出f(x)在R上是增函数.(3)解此不等式第一个关键是确定f(1)+f(1)=f(2)=4,然后不等式
 ,再利用f(x)在R上是增函数,脱掉法则符号f,转化为关于x的二次不等式求解即可.
,再利用f(x)在R上是增函数,脱掉法则符号f,转化为关于x的二次不等式求解即可.解:1)
 有
有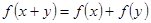
令
 得
得 又令
又令 得
得 即
即 解得
解得 …………14分
…………14分
练习册系列答案
相关题目
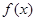 是定义在
是定义在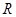 上的偶函数,且
上的偶函数,且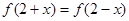 ,当
,当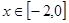 时,
时,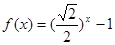 ,若在区间
,若在区间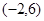 内关于
内关于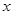 的方程
的方程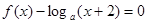 ,恰有
,恰有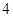 个不同的实数根,则实数
个不同的实数根,则实数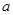
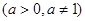 的取值范围是
的取值范围是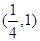
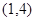
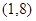
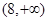
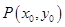 是函数
是函数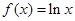 图象上一点,过点
图象上一点,过点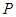 的切线与
的切线与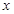 轴交于
轴交于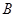 ,过点
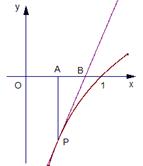
,过点 .
.
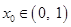 ,求
,求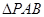 的面积
的面积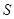 的最大值,并求此时
的最大值,并求此时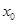 的值.
的值.
 ,
,  ,且关于x的方程
,且关于x的方程 有2个不等实数根
有2个不等实数根 、
、 ,则
,则


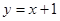
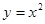
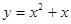
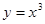
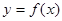 ,
,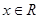 ,有下列4个命题:
,有下列4个命题: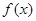 为偶函数,且
为偶函数,且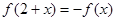 ,则
,则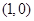 中心对称;
中心对称;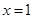 对称,则
对称,则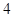 为函数
为函数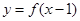 与
与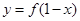 的图象关于直线
的图象关于直线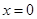 对称;
对称;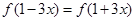 ,则
,则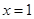 对称;
对称;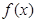 是定义在
是定义在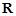 上的奇函数,且当
上的奇函数,且当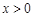 时,
时,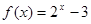 ,则
,则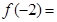 .
.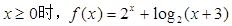 则f (-1)=
则f (-1)= 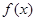 满足
满足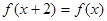 ,且当
,且当 时,
时, 的值为 。
的值为 。