题目内容
已知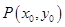 是函数
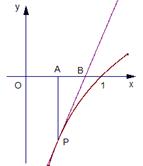
是函数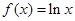 图象上一点,过点
图象上一点,过点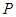 的切线与
的切线与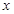 轴交于
轴交于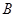 ,过点
,过点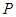 作
作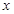 轴的垂线,垂足为
轴的垂线,垂足为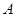 .
.
(1)求点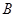 坐标;
坐标;
(2)若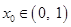 ,求
,求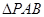 的面积
的面积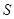 的最大值,并求此时
的最大值,并求此时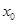 的值.
的值.
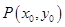 是函数
是函数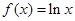 图象上一点,过点
图象上一点,过点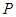 的切线与
的切线与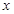 轴交于
轴交于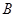 ,过点
,过点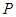 作
作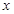 轴的垂线,垂足为
轴的垂线,垂足为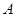 .
.
(1)求点
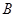 坐标;
坐标;(2)若
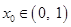 ,求
,求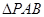 的面积
的面积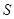 的最大值,并求此时
的最大值,并求此时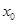 的值.
的值.(1)点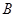 的坐标为
的坐标为
(2)当 ,面积
,面积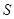 的最大值为
的最大值为 .
.
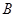 的坐标为
的坐标为
(2)当
 ,面积
,面积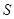 的最大值为
的最大值为 .
.本试题主要是考查了导数的几何意义的运用,以及三角形面积公式的求解和函数的单调性的运用。
(1)因为 , ∴ 过点
, ∴ 过点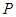 的切线方成为
的切线方成为 ,点斜式得到结论。
,点斜式得到结论。
(2) ,
,
∴ 进而求解的得到最值。
进而求解的得到最值。
(1)因为
 , ∴ 过点
, ∴ 过点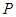 的切线方成为
的切线方成为 ,点斜式得到结论。
,点斜式得到结论。(2)
 ,
,
∴
 进而求解的得到最值。
进而求解的得到最值。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
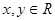 有
有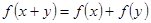
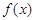 的奇偶性;
的奇偶性;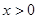 时,
时,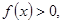 证明:
证明: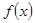 在
在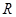 上为增函数;
上为增函数;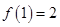 ,解不等式:
,解不等式: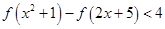
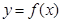 是定义在R上的奇函数,当
是定义在R上的奇函数,当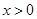 时,
时,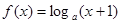 (其中
(其中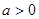 且
且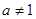 )
)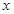 为何值时,
为何值时,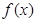 的值的小于0?
的值的小于0?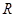 上的函数
上的函数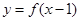 的图像关于
的图像关于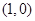 对称,且当
对称,且当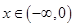 时,
时,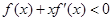 (其中
(其中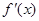 是
是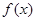 的导函数),若
的导函数),若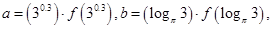
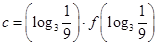 ,则
,则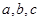 的大小关系是( )
的大小关系是( )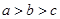
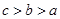
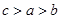
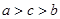
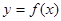
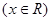 满足
满足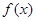 是偶函数,又
是偶函数,又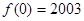 ,
,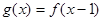 为奇函数,则
为奇函数,则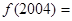 _______
_______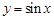
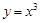
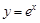
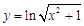
 则关于
则关于 的方程
的方程 上解的个数是 个.
上解的个数是 个.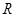 上的偶函数
上的偶函数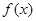 满足
满足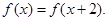 当
当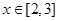 时,
时,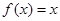 ,则
,则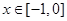 时,
时,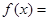 ________.
________. 是定义在R上的奇函数,满足
是定义在R上的奇函数,满足 ,当
,当 时,
时, ,
, 的值等于( )
的值等于( )
