题目内容
已知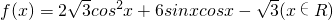 ,
,
(1)求函数f(x)的单调递减区间,并指出函数y=f(x)的图象是由函数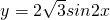 的图象经过怎样的变换得到的;
的图象经过怎样的变换得到的;
(2)当 时,求函数f(x)的最值,并求出函数取最值时的x的值.
时,求函数f(x)的最值,并求出函数取最值时的x的值.
解:(1)f(x)= (1+cos2x)+3sin2x-
(1+cos2x)+3sin2x-
= (cos2x+
(cos2x+ sin2x)
sin2x)
=2 sin(2x+
sin(2x+ )
)
 +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ,k∈Z
+2kπ,k∈Z
∴f(x)的单调减区间[ +kπ,
+kπ, +kπ],k∈Z
+kπ],k∈Z
y=2 sin2x向左平移
sin2x向左平移 得到y=2
得到y=2 sin(2x+
sin(2x+ )
)
(2)∵x∈[0, ]
]
∴2x+ ∈[
∈[ ,
, ]
]
∴sin(2x+ )∈[-
)∈[- ,1]
,1]
∴当2x+ =
= ,即x=
,即x= 时,f(x)min=-
时,f(x)min=- ,
,
当2x+ =
= ,即x=
,即x= 时,f(x)max=2
时,f(x)max=2 .
.
分析:(1)利用两角和差的三角函数化简函数,得到y=2 sin(2x+
sin(2x+ ),进而得到单调递减区间;y=2
),进而得到单调递减区间;y=2 sin2x向左平移
sin2x向左平移 得到y=2
得到y=2 sin(2x+
sin(2x+ );
);
(2)当 时,,求出2x+
时,,求出2x+ 的范围,进而得到sin(2x+
的范围,进而得到sin(2x+ )的范围,从而得到函数f(x)的 范围,从而求得函数f(x)的最大值.
)的范围,从而得到函数f(x)的 范围,从而求得函数f(x)的最大值.
点评:本题考查两角和差的三角函数,求三角函数的值域,求三角函数的值域是解题的难点.
 (1+cos2x)+3sin2x-
(1+cos2x)+3sin2x-
=
 (cos2x+
(cos2x+ sin2x)
sin2x)=2
 sin(2x+
sin(2x+ )
) +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ,k∈Z
+2kπ,k∈Z∴f(x)的单调减区间[
 +kπ,
+kπ, +kπ],k∈Z
+kπ],k∈Zy=2
 sin2x向左平移
sin2x向左平移 得到y=2
得到y=2 sin(2x+
sin(2x+ )
)(2)∵x∈[0,
 ]
]∴2x+
 ∈[
∈[ ,
, ]
]∴sin(2x+
 )∈[-
)∈[- ,1]
,1]∴当2x+
 =
= ,即x=
,即x= 时,f(x)min=-
时,f(x)min=- ,
,当2x+
 =
= ,即x=
,即x= 时,f(x)max=2
时,f(x)max=2 .
.分析:(1)利用两角和差的三角函数化简函数,得到y=2
 sin(2x+
sin(2x+ ),进而得到单调递减区间;y=2
),进而得到单调递减区间;y=2 sin2x向左平移
sin2x向左平移 得到y=2
得到y=2 sin(2x+
sin(2x+ );
);(2)当
 时,,求出2x+
时,,求出2x+ 的范围,进而得到sin(2x+
的范围,进而得到sin(2x+ )的范围,从而得到函数f(x)的 范围,从而求得函数f(x)的最大值.
)的范围,从而得到函数f(x)的 范围,从而求得函数f(x)的最大值.点评:本题考查两角和差的三角函数,求三角函数的值域,求三角函数的值域是解题的难点.

练习册系列答案
相关题目
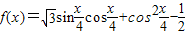 .
.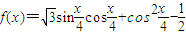 .
.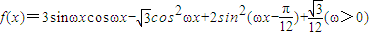 .
.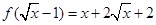 ,
,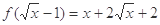 ,
,