题目内容
已知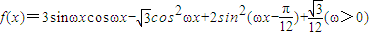 .
.(1)求函数f(x)值域;
(2)若对任意的a∈R,函数y=f(x)在(a,a+π]上的图象与y=1有且仅有两个不同的交点,试确定ω的值(不必证明)并写出该函数在[0,π]上的单调区间.
【答案】分析:(1)利用三角函数的恒等变换化简f(x)的解析式为 ,由正弦函数的值域从而得到f(x)值域.
,由正弦函数的值域从而得到f(x)值域.
(2)由题意可得f(x)周期为π,求出ω=1,从而得到 ,由此写出函数在[0,π]上的单调区间.
,由此写出函数在[0,π]上的单调区间.
解答:解:(1)f(x)=
=
= (2分)
(2分)
=
= . (6分)
. (6分)
∴f(x)值域为[-1,3].
(2)由题意可得 f(x)周期为π,∴ω=1.(8分) 故 ,
,
故 f(x)在 、
、 上单调递增,在
上单调递增,在 上单调递减.(12分)
上单调递减.(12分)
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的值域和单调性,化简函数f(x)的解析式为 ,是解题的关键.
,是解题的关键.
 ,由正弦函数的值域从而得到f(x)值域.
,由正弦函数的值域从而得到f(x)值域.(2)由题意可得f(x)周期为π,求出ω=1,从而得到
 ,由此写出函数在[0,π]上的单调区间.
,由此写出函数在[0,π]上的单调区间.解答:解:(1)f(x)=

=

=
 (2分)
(2分)=

=
 . (6分)
. (6分)∴f(x)值域为[-1,3].
(2)由题意可得 f(x)周期为π,∴ω=1.(8分) 故
 ,
,故 f(x)在
 、
、 上单调递增,在
上单调递增,在 上单调递减.(12分)
上单调递减.(12分)点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的值域和单调性,化简函数f(x)的解析式为
 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目
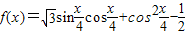 .
.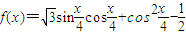 .
.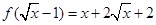 ,
,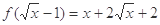 ,
,