题目内容
13.某购物网站为了解顾客对某商品的满意度,随机调查50名顾客对该商品的评价,具体数据如下| 评分 | 1 | 2 | 3 | 4 | 5 |
| 人数 | x | 20 | 10 | 5 | y |
(Ⅰ)求x与y的值;
(Ⅱ)若将频率视为概率,现从对该商品作出了评价的顾客中,随机抽取一位,记该顾客的评分为X,求随机变量X的分布列一与数学期望.
分析 (Ⅰ)列出题意:x+20+10=50×80%,5+y=50×20%,即可求解.
(Ⅱ)确定随机变量,分别求解概率,列出分布列,运用公式求解X的数学期望.
解答 解:(Ⅰ)依题意得,x+20+10=50×80%,5+y=50×20%,
解得x=10,y=5.…(6分)
(Ⅱ)$P(X=1)=\frac{10}{50}=0.2$,$P(X=2)=\frac{20}{50}=0.4$,$P(X=3)=\frac{10}{50}=0.2$,$P(X=4)=\frac{5}{50}=0.1$,$P(X=5)=\frac{5}{50}=0.1$…(10分)
所以X的分布列为
| X | 1 | 2 | 3 | 4 | 5 |
| P | 0.2 | 0.4 | 0.2 | 0.1 | 0.1 |
点评 本题考查了离散型的概率分布,数学期望,仔细阅读理解题意,利用排列组合知识求解,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知f(x)=x2-2x,g(x)=x-2,则f[g(2)]与g[f(2)]的大小关系是( )
| A. | f[g(2)]>g[f(2)] | B. | f[g(2)]=g[f(2)] | C. | f[g(2)]<g[f(2)] | D. | 无法确定 |
1.执行下列程序,则输出的S的值是( )


| A. | $-1-\frac{{\sqrt{2}}}{2}$ | B. | -1 | C. | 0 | D. | $\frac{{\sqrt{2}}}{2}$ |
2.已知sin α-3cos α=0,则$\frac{sin2α}{co{s}^2α-si{n}^2α}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
3.函数f(x)=-2x+3,x∈[-2,3)的值域是( )
| A. | [-1,3) | B. | [-3,7) | C. | (-1,3] | D. | (-3,7] |
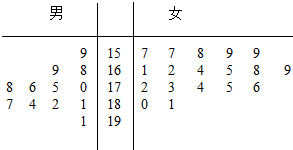 第4届湘台经贸洽谈交流会于2011年6月在我市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.(I)如果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?(Ⅱ)若从所有“高个子”中选3名志愿者,用X表示所选志愿者中能担任“礼仪小姐”的人数,试写出X的分布列,并求X的数学期望.
第4届湘台经贸洽谈交流会于2011年6月在我市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.(I)如果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?(Ⅱ)若从所有“高个子”中选3名志愿者,用X表示所选志愿者中能担任“礼仪小姐”的人数,试写出X的分布列,并求X的数学期望.