题目内容
一个正三棱柱的三视图如图所示，其中侧视图是一个长为4| 3 |
分析：由三视图中的数据知道，棱柱的高是4，底面正三角形的高是4
，由此可以解出底面正三角形的边长，再由公式求出其表面积与体积即可．
| 3 |
解答：
解：由三视图可知正三棱柱的高为4，
由侧视图知正三棱柱的底面三角形的高为4
，
设底面边长为a，则
a=4
，∴a=8，
∴S棱柱底=
•82=16
；S棱柱侧=（3•8）•4=96，
∴正三棱柱的表面积 S=S侧+2S底=96+32
，
∴正三棱柱的体积 V柱=(
•82)•4=64
．
解：由三视图可知正三棱柱的高为4，由侧视图知正三棱柱的底面三角形的高为4
| 3 |
设底面边长为a，则
| ||
| 2 |
| 3 |
∴S棱柱底=
| ||
| 4 |
| 3 |
∴正三棱柱的表面积 S=S侧+2S底=96+32
| 3 |
∴正三棱柱的体积 V柱=(
| ||
| 4 |
| 3 |
点评：本题考查由三视图求表面积与体积，考查由三视图复原实物图度量的能力，以及利用公式求表面积与体积的能力．
练习册系列答案
相关题目
一个正三棱柱的三视图如图所示，则这个正三棱柱的体积是若一个正三棱柱的三视图如下，且铡视图长为
，宽为2：则这个正三棱柱的体积为（ ）
| 3 |
A、6
| ||||
B、2
| ||||
C、8
| ||||
D、
|
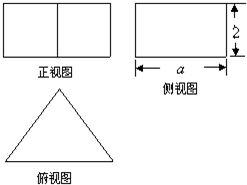如图是一个正三棱柱的三视图，若三棱柱的体积是1，则a=
如图是一个正三棱柱的三视图，若三棱柱的体积是