题目内容

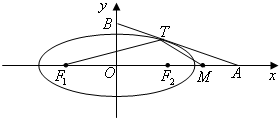
如图：从椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)上一点M向x轴作垂线，恰好通过椭圆的左焦点F1（-c，0），且
.
AB
∥
.
OM
，则a，b，c必满足______．
∵MF1⊥x轴，∴设M（-c，y0），代入椭圆方程可得
c2
a2
+
y02
b2
=1，
因此y0=
b2
a
（舍负），可得|MF1|=
b2
a

∵
.
AB
∥
.
OM
，
∴△ABO∽△OMF1，可得
|MF1|
|OB|
=
|OF1|
|AO|
，即
b2
a
b
=
c
a

解之得b=c，结合a2=b2+c2得b=c=
2
2
a
∴椭圆的离心率e=
c
a
=
2
2

故答案为：b=c=
2
2
a
练习册系列答案
相关题目
已知椭圆以对称轴为坐标轴，且长轴是短轴的3倍，并且过点（3，0），求椭圆的标准方程．
已知椭圆C1，抛物线C2的焦点均在y轴上，C1的中心和C2的顶点均为坐标原点O，从每条曲线上取两个点，将其坐标记录于下表中：
x0-1
2
4
y-2
2
1
16
-21
（Ⅰ）求分别适合C1，C2的方程的点的坐标；
（Ⅱ）求C1，C2的标准方程．
设F1，F2分别是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点，若在直线x=
a2
c
上存在点P，使线段PF1的中垂线过点F2，则椭圆的离心率的取值范围是______．
已知直线l：y=kx+2（k为常数）过椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的上顶点B和左焦点F，且被圆x2+y2=4截得的弦长为L，若L≥
4
5
5
，则椭圆离心率e的取值范围是（　　）
A．(0，
5
5
]		B．(0，
2
5
5
]		C．(0，
3
5
5
]		D．(0，
4
5
5
]
求以椭圆
x2
16
+
y2
9
=1的短轴的两个端点为焦点，且过点A（4，-5）的双曲线的标准方程．
如图，椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）与过A（2，0），B（0，1）的直线有且只有一个公共点T，且椭圆的离心率e=
3
2

（1）求椭圆方程；
（2）设F1、F2分别为椭圆的左、右焦点，M为线段AF2的中点，求tan∠ATM．
设点P是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)与圆x2+y2=3b2的一个交点，F1，F2分别是椭圆的左、右焦点，且|PF1|=3|PF2|，则椭圆的离心率为（　　）
A．
10
4
B．
3
5
C．
7
4
D．
14
4
设椭圆
x2
a2
+
y2
b2
=1的两焦点为F1、F2，长轴两端点为A1、A2．
（1）P是椭圆上一点，且∠F1PF2=60°，求△F1PF2的面积；
（2）若椭圆上存在一点Q，使∠A1QA2=120°，求椭圆离心率e的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网