题目内容
8.若有关x的方程x2lnx=kx-1有实数解,则实数k的取值范围为( )| A. | (-∞,-1]∪[1,+∞) | B. | (-∞,-1] | C. | [1,+∞) | D. | (-∞,-1]∪(1,+∞) |
分析 化简可得k=xlnx+$\frac{1}{x}$,令f(x)=xlnx+$\frac{1}{x}$,从而求导可得f′(x)=lnx+1-$\frac{1}{{x}^{2}}$;从而判断函数的单调性及最值,从而求实数k的取值范围.
解答 解:∵x2lnx=kx-1,
∴k=xlnx+$\frac{1}{x}$,
令f(x)=xlnx+$\frac{1}{x}$,则f′(x)=lnx+1-$\frac{1}{{x}^{2}}$;
故当x∈(0,1)时,f′(x)<0;
当x∈(1,+∞)时,f′(x)>0;
故f(x)min=f(1)=1•ln1+1=1,
故实数k的取值范围为[1,+∞);
故选:C.
点评 本题考查了导数的综合应用及函数的最值,同时考查了方程与函数的关系应用.

练习册系列答案
相关题目
20.已知a为锐角,且cos($α+\frac{π}{4}$)=$\frac{3}{5}$,则tanα=( )
| A. | 7 | B. | $\frac{1}{7}$ | C. | -7 | D. | $-\frac{1}{7}$ |
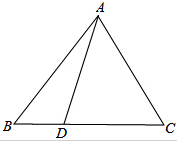 如图,△ABC中,|AB|=|AC|,D是BC边上任意一点,(D与B、C不重合),求证:|AB|2=|AD|2+|BD|•|DC|.
如图,△ABC中,|AB|=|AC|,D是BC边上任意一点,(D与B、C不重合),求证:|AB|2=|AD|2+|BD|•|DC|.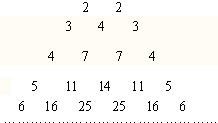 如图,它满足(1)第n行首尾两数均为n,
如图,它满足(1)第n行首尾两数均为n,