题目内容
11.若(1-$\frac{1}{{x}^{2}}$)n(n∈N*,n>1)的展开式中x-4的系数为an,则$\frac{1}{{a}_{2}}+\frac{1}{{a}_{3}}+…+\frac{1}{{a}_{n}}$为( )| A. | $\frac{n-1}{n}$ | B. | $\frac{2n-2}{n}$ | C. | $\frac{1-n}{n}$ | D. | $\frac{2-2n}{n}$ |
分析 根据通项公式求得展开式中x-4的系数为an =${C}_{n}^{2}$=$\frac{n(n-1)}{2}$,可得$\frac{1}{{a}_{n}}$=2($\frac{1}{n-1}$-$\frac{1}{n}$),从而求得要求式子的值.
解答 解:(1-$\frac{1}{{x}^{2}}$)n(n∈N*,n>1)的展开式的通项公式为 Tr+1=${C}_{n}^{r}$•(-1)r•x-2r,
故展开式中x-4的系数为an =${C}_{n}^{2}$=$\frac{n(n-1)}{2}$,∴$\frac{1}{{a}_{n}}$=2($\frac{1}{n-1}$-$\frac{1}{n}$),
∴$\frac{1}{{a}_{2}}+\frac{1}{{a}_{3}}+…+\frac{1}{{a}_{n}}$=2[(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{n-1}$-$\frac{1}{n}$)]=2(1-$\frac{1}{n}$)=$\frac{2n-2}{n}$,
故选:B.
点评 本题主要考查二项式定理的应用,求展开式中某项的系数,用裂项法进行求和,属于基础题.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
1.已知等差数列{an}中,a4+a7=42,则前10项和S10=( )
| A. | 420 | B. | 380 | C. | 210 | D. | 140 |
2.在△ABC中,若2cosB•sinA=sinC,则△ABC一定是( )三角形.
| A. | 等腰 | B. | 直角 | C. | 等边 | D. | 等腰直角 |
6.若变量x,y满足:$\left\{\begin{array}{l}{2x-y+2≤0}\\{x+2y-4≥0}\\{x-3y+11≥0}\end{array}\right.$,且满足(t+1)x+(t+2)y+t=0,则参数t的取值范围为( )
| A. | -2<t<-$\frac{4}{3}$ | B. | -2<t≤-$\frac{4}{3}$ | C. | -2≤t≤-$\frac{4}{3}$ | D. | -2≤t<-$\frac{4}{3}$ |
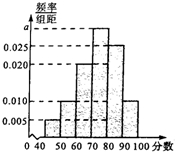 某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.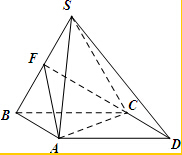 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2$\sqrt{2}$,SB=SC=AB=2,F为线段SB的中点.
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2$\sqrt{2}$,SB=SC=AB=2,F为线段SB的中点.