题目内容
16.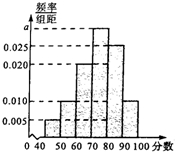 某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.(Ⅰ)求图中实数a的值;
(Ⅱ)根据频率分布直方图,试估计该校高一年级学生其中考试数学成绩的平均数;
(Ⅲ)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.
分析 (Ⅰ)由频率分布直方图中频率之和为1,能求出a.
(Ⅱ)平均分是频率分布直方图各个小矩形的面积×底边中点横坐标之和,由此利用频率分布直方图能求出平均分.
(Ⅲ)由频率分布直方图,得数学成绩在[40,50)内的学生人数为40×0.05=2,这两人分别记为A,B,数学成绩在[90,100)内的学生人数为40×0.1=4,这4人分别记为C,D,E,F,如果这两名学生的数学成绩都在[40,50)或都在[90,100)内,则这两名学生的数学成绩之差的绝对值不大于10,由此利用列举法能过河卒子同这两名学生的数学成绩之差的绝对值不大于10的概率.
解答 解:(Ⅰ)由频率分布直方图,得:
10×(0.005+0.01+0.025+a+0.01)=1,
解得a=0.03.
(Ⅱ)由频率分布直方图得到平均分:
$\overline{x}$=0.05×45+0.1×55+0.2×65+0.3×75+0.25×85+0.1×95=74(分).
(Ⅲ)由频率分布直方图,得数学成绩在[40,50)内的学生人数为40×0.05=2,这两人分别记为A,B,
数学成绩在[90,100)内的学生人数为40×0.1=4,这4人分别记为C,D,E,F,
若从数学成绩在[40,50)与[90,100)两个分数段内的学生中随机选取2名学生,
则所有的基本事件有:
(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),
(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15个,
如果这两名学生的数学成绩都在[40,50)或都在[90,100)内,
则这两名学生的数学成绩之差的绝对值不大于10,
记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,
则事件M包含的基本事件有:(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共7个,
所以这两名学生的数学成绩之差的绝对值不大于10的概率P=$\frac{7}{15}$.
点评 本题考查频率和概率的求法,二查平均分的求法,是中档题,解题时要认真审题,注意频率分布直方图和列举法的合理运用.

| A. | 0.16 | B. | 0.32 | C. | 0.68 | D. | 0.84 |
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
| A. | $\frac{n-1}{n}$ | B. | $\frac{2n-2}{n}$ | C. | $\frac{1-n}{n}$ | D. | $\frac{2-2n}{n}$ |
| A. | M-N=4 | B. | M+N=4 | C. | M-N=2 | D. | M+N=2 |