题目内容

已知点P(x，y)满足
x-4y+3≤0
3x+5y≤25
x-1≥0
，A(2，0)，则|
OP
|sin∠AOP（O为坐标原点）的最大值为（　　）
A、
22
5
B、2
C、1
D、0
分析：画出不等式组的可行域，判断出目标函数的几何意义，结合图象得到最大值．
解答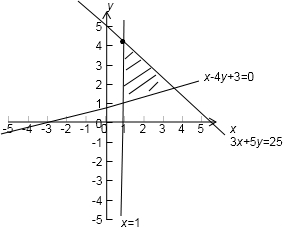：精英家教网解：画出可行域，
根据题意，分析可得：|
OP
|sin∠AOP表示的是点P的纵坐标，
由图知，可行域中点（1，
22
5
）的纵坐标最大，
故选A
点评：本题考查画不等式组表示的平面区域、关键给目标函数几何意义、数形结合的数学思想方法．
练习册系列答案
相关题目
已知点P在抛物线y=
1
4
x2上，若点P到x轴的距离与点P到抛物线焦点F的距离之比为
1
3
，则点P到焦点F的距离是（　　）
A、
1
2
B、
3
32
C、
1
32
D、
3
2
已知点P在曲线y=
1
3
x3-x+
2
3
上移动，若经过点P的曲线的切线的倾斜角为α，则α的取值范围是
 
．
已知点P是曲线C：
x=2
3
cosθ
y=2sinθ
（θ为参数）上一点，且在第一象限，OP（O是平面直角坐标系的原点）的倾斜角为
π
6
，则点P的坐标为（　　）
A、（
6
，
2
）
B、（
3
，1）
C、（
2
，
6
）
D、（1，
3
）
（2011•惠州模拟）已知点P是圆F1：(x+1)2+y2=8上任意一点，点F2与点F1关于原点对称．线段PF2的中垂线m分别与PF1、PF2交于M、N两点．
（1）求点M的轨迹C的方程；
（2）斜率为k的直线l与曲线C交于P，Q两点，若
OP
•
OQ
=0（O为坐标原点），试求直线l在y轴上截距的取值范围．
已知点P在曲线y=
1
3
x3-x+
2
3
上移动，若经过点P的曲线的切线的倾斜角为α，则α的取值范围是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网