题目内容
如图5，三棱锥P—ABC中， PC
平面ABC，PC=AC=2，
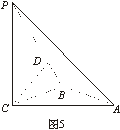AB=BC，D是PB上一点，且CD平面PAB．
（1）求证：AB平面PCB；
（2）求异面直线AP与BC所成角的大小；
（3）求二面角C—PA—B的大小的余弦值．
解：（1）将椭圆E的方程化为标准方程：
， （1分）
于是
，
，
，
因此，椭圆E的长轴长为
，短轴长为
，离心率
，两个焦点坐标分别是F1（0，-1）、F2（0，1），四个顶点的坐标分别是
，
，
和
. （6分）
（2）依题意，不妨设直线l过F2（0，1）与椭圆E的交点
，
则
. （8分）
根据题意，直线l的方程可设为
，
将代入
，得
.
由韦达定理得：
， （10分）
所以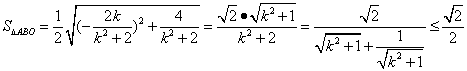
（当且仅当
，即
时等号成立）. （13分）
故DABO的面积的最大值为
. （14分）
练习册系列答案
相关题目
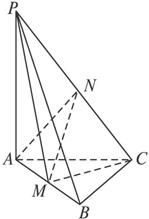
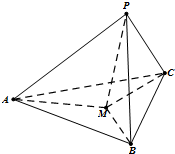如图，在三棱锥P-ABC中，PA，PB，PC两两垂直，且PA=5，PB=4，PC=3．设点M为底面ABC内一点，定义f（M）=（m，n，p），其中m，n，p分别为三棱锥M-PAB、M-PBC、M-PCA的体积．若f（M）=（4，3x，3y），且ax-8xy+y≥0恒成立，则正实数a的取值范围是
如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF=
