题目内容
4.若体积为4的长方体的一个面的面积为1,且这个长方体8个顶点都在球O的球面上,则球O表面积的最小值为18π.分析 设长方体的三度为a,b,c,则ab=1,abc=4,可得c=4,长方体的对角线的长度,就是外接球的直径,求出直径的最小值,即可求出球O表面积的最小值.
解答 解:设长方体的三度为a,b,c,则ab=1,abc=4,∴c=4.
长方体的对角线的长度,就是外接球的直径,所以2r=$\sqrt{{a}^{2}+{b}^{2}+16}$≥$\sqrt{2ab+16}$=3$\sqrt{2}$,
当且仅当a=b时,r的最小值为$\frac{3\sqrt{2}}{2}$,
所以球O表面积的最小值为:4πr2=18π.
故答案为:18π.
点评 本题是基础题,考查长方体的外接球的应用,球的表面积的求法,考查计算能力.

练习册系列答案
相关题目
12.已知定义在(0,+∞)上连续可导的函数f(x)满足xf'(x)+f(x)=x,且f(1)=1,则( )
| A. | f(x)是增函数 | B. | f(x)是减函数 | C. | f(x)有最大值1 | D. | f(x)有最小值1 |
13.已知函数y=5cos($\frac{2k+1}{3}$πx-$\frac{π}{6}$)(其中k∈N),对任意实数a,在区间[a,a+3]上要使函数值$\frac{5}{4}$出现的次数不少于4次且不多于8次,则k值为( )
| A. | 2或3 | B. | 4或3 | C. | 5或3 | D. | 8或3 |
12.若直线l∥平面α,直线a?α,则l与α的位置关系是( )
| A. | l∥α | B. | l与α异面 | C. | l与α相交 | D. | l与α没有公共点 |
16.设f(x)是定义在R上的偶函数,且f(2+x)=f(2-x),当x∈[-2,0]时,f(x)=($\frac{\sqrt{2}}{2}$)x-1,若在区间(-2,6)内关于x的方程f(x)-log a(x+2)=0,恰有4个不同的实数根,则实数a(a>0,a≠1)的取值范围是( )
| A. | ($\frac{1}{4}$,1) | B. | (1,4) | C. | (1,8) | D. | (8,+∞) |
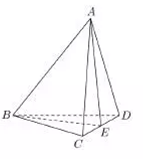 如图,三棱锥A-BCD中,△BCD为等边三角形,AC=AD,E为CD的中点;
如图,三棱锥A-BCD中,△BCD为等边三角形,AC=AD,E为CD的中点;