题目内容
设数列{an}满足an+1=2an+n2-4n+1.
(1)若a1=3,求证:存在f(n)=an2+bn+c(a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(2)若an是一个等差数列{bn}的前n项和,求首项a1的值与数列{bn}的通项公式.
(1)若a1=3,求证:存在f(n)=an2+bn+c(a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(2)若an是一个等差数列{bn}的前n项和,求首项a1的值与数列{bn}的通项公式.
考点:等比数列的性质,等比关系的确定
专题:等差数列与等比数列
分析:(1)设an+1 +a(n+1)2+b(n+1)+c=2(an+an2+bn+c),即 an+1=2an+an2+(b-2a)n+c-a-b,
由已知得
,求得a、b、c的值,可得存在f(n)=n2-2n,从而求得 an 的解析式.
(2)由可得(an+n2-2n)=(a1-1)•2n-1,即 an=-n2+2n+(a1-1)•2n-1,再根据an是一个等差数列{bn}的前n项和,求出求首项a1的值与数列{bn}的通项公式.
由已知得
|
(2)由可得(an+n2-2n)=(a1-1)•2n-1,即 an=-n2+2n+(a1-1)•2n-1,再根据an是一个等差数列{bn}的前n项和,求出求首项a1的值与数列{bn}的通项公式.
解答:
解:(1)∵数列{an}满足an+1=2an+n2-4n+1,
设an+1 +a(n+1)2+b(n+1)+c=2(an+an2+bn+c),即 an+1=2an+an2+(b-2a)n+c-a-b,
∴
,即
.
∵a1+1-2=2,∴存在f(n)=n2-2n,使数列{an+f(n)}是等比数列,
∴an+n2-2n=2×2n-1,
∴an=2n-n2+2n.
(2)∵an是一个等差数列{bn}的前n项和,数列{an}满足an+1=2an+n2-4n+1,
即 an+1 +(n+1)2-2(n+1)=2(an+n2-n ),
即an+1+(n+1)2-2(n+1)=2(an+n2-2n),
∴(an+n2-2n)=(a1-1)•2n-1,故an=-n2+2n+(a1-1)•2n-1,
∴bn=
.
再根据{bn}是等差数列,可得bn的通项公式是关于n的一次函数,
∴a1=1,an=-2n+3.
设an+1 +a(n+1)2+b(n+1)+c=2(an+an2+bn+c),即 an+1=2an+an2+(b-2a)n+c-a-b,
∴
|
|
∵a1+1-2=2,∴存在f(n)=n2-2n,使数列{an+f(n)}是等比数列,
∴an+n2-2n=2×2n-1,
∴an=2n-n2+2n.
(2)∵an是一个等差数列{bn}的前n项和,数列{an}满足an+1=2an+n2-4n+1,
即 an+1 +(n+1)2-2(n+1)=2(an+n2-n ),
即an+1+(n+1)2-2(n+1)=2(an+n2-2n),
∴(an+n2-2n)=(a1-1)•2n-1,故an=-n2+2n+(a1-1)•2n-1,
∴bn=
|
再根据{bn}是等差数列,可得bn的通项公式是关于n的一次函数,
∴a1=1,an=-2n+3.
点评:本题主要考查等差数列的定义和性质,等比关系的确定,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
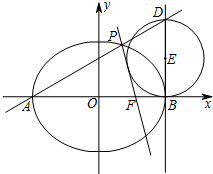 已知椭圆C的中心在坐标原点,右焦点为F(1,0),A、B是椭圆C的左、右顶点,P是椭圆C上异于A、B的动点,且△APB面积的最大值为2
已知椭圆C的中心在坐标原点,右焦点为F(1,0),A、B是椭圆C的左、右顶点,P是椭圆C上异于A、B的动点,且△APB面积的最大值为2