题目内容
11．设g（x）=$\left\{\begin{array}{l}{{e}^{x}，x≤0}\\{lnx，x＞0}\end{array}\right.$，则关于x的不等式g（x）≤1的解是（ ）| A． | （-∞，e] | B． | （-∞，1] | C． | [0，e] | D． | [0，1] |
分析 结合指数函数和对数函数的图象和性质，分类讨论不等式g（x）≤1的解，综合讨论结果可得答案．
解答 解：当x≤0时，解不等式g（x）=ex≤1得：x≤0；
当x＞0时，解不等式g（x）=lnx≤1得：0＜x≤e；
综上所述，不等式g（x）≤1的解集是：（-∞，e]，
故选：A．
点评 本题考查的知识点是分段函数的应用，指数函数和对数函数的图象和性质，分类讨论思想，难度中档．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
6．任取k∈[-1，1]，直线L：y=kx+3与圆C：（x-2）2+（y-3）2=4相交于M、N两点，则|MN|≥2$\sqrt{3}$的概率为 （ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{2}$ |
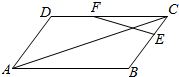如图，在?ABCD中，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，$\overrightarrow{CE}$=$\frac{1}{3}$$\overrightarrow{CB}$，$\overrightarrow{CF}$=$\frac{2}{3}$$\overrightarrow{CD}$．