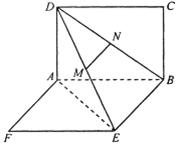
题目内容
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为30°、45°, M、N分别为DE与DB的中点,且MN=1。
(Ⅰ)求证:MN⊥平面ABCD;
(Ⅱ)求线段AB的长;
(Ⅲ)求二面角A-DE-B的平面角的正弦值。
(Ⅰ)求证:MN⊥平面ABCD;
(Ⅱ)求线段AB的长;
(Ⅲ)求二面角A-DE-B的平面角的正弦值。

| (Ⅰ)证明:∵平面ABCD⊥平面ABEF,且平面ABCD∩平面ABEF=AB,EB⊥AB, ∴EB⊥平面ABCD, 又MN∥EB, ∴MN⊥面ABCD. |
|
| (Ⅱ)解:由(Ⅰ)可知∠EDB为DE与平面ABCD所成的角, ∴∠EDB=30°, 又在Rt△EBD中,EB=2MN=2,∠EBD=90°, ∴DE=  , ,连结AE,可知∠DEA为DE与平面ABEF所成的角, ∴∠DEA=45°, 在Rt△DAE中,∠DAE=90°, ∴AE=DE·cos∠DEA=2  , ,在Rt△ABE中,  。 。 (Ⅲ)解:过B作BO⊥AE于O点,过O作OH⊥DE于H,连BH, ∵AD⊥平面ABEF,BO  面ABEF, 面ABEF,∴BO⊥平面ADE, ∴OH为BH在平面ADE内的射影, ∴BH⊥DE,即∠BHO为所求二面角的平面角, 在Rt△ABE中,BO=  , ,在Rt△DBE中,由BH·DE=DB·OE得BH=  , ,∴sin∠BHO=  。 。 |
 |

练习册系列答案
相关题目
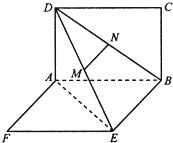 如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为300、450,M、N分别为DE与DB的中点,且MN=1.
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为300、450,M、N分别为DE与DB的中点,且MN=1.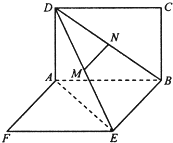 (2012•焦作模拟)如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.
(2012•焦作模拟)如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.
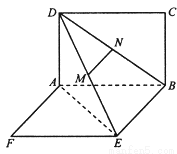
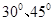 ,M、N分别为DE与DB的中点,且MN=1.
,M、N分别为DE与DB的中点,且MN=1.