题目内容
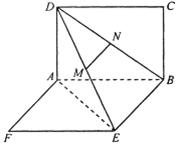
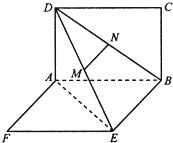 如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为300、450,M、N分别为DE与DB的中点,且MN=1.
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为300、450,M、N分别为DE与DB的中点,且MN=1.(I) 求证:MN⊥平面ABCD
(II) 求线段AB的长;
(III)求二面角A-DE-B的平面角的正弦值.
分析:(Ⅰ) 先证明 EB⊥平面ABCD,由三角形的中位线的性质可得MN∥EB,故MN⊥面ABCD.
(Ⅱ)利用直角三角形中的边角关系求得DE,进而求得AE,在Rt△ABE中,由勾股定理求得AB的长.
(Ⅲ)过B作BO⊥AE于O点,过O作OH⊥DE于H,连BH,由三垂线定理可证∠BHO为所求二面角的平面角,用面积法求出BO和 BH,由 sin∠BHO=
求得二面角A-DE-B的平面角的正弦值.
(Ⅱ)利用直角三角形中的边角关系求得DE,进而求得AE,在Rt△ABE中,由勾股定理求得AB的长.
(Ⅲ)过B作BO⊥AE于O点,过O作OH⊥DE于H,连BH,由三垂线定理可证∠BHO为所求二面角的平面角,用面积法求出BO和 BH,由 sin∠BHO=
| BO |
| BH |
解答: 解:(Ⅰ)证明:∵平面ABCD⊥平面ABEF,且平面ABCD∩平面ABEF=AB,
解:(Ⅰ)证明:∵平面ABCD⊥平面ABEF,且平面ABCD∩平面ABEF=AB,
EB⊥AB,∴EB⊥平面ABCD,又MN∥EB,∴MN⊥面ABCD.
(Ⅱ)由(Ⅰ)可知∠EDB为DE与平面ABCD所成的角,∴∠EDB=30°.
又在Rt△EBD中,EB=2MN=2,∠EBD=90°∴DE=
=4,
连接AE,可知∠DEA为DE与平面ABEF所成的角,∴∠DEA=45°.
在Rt△DAE中,∠DAE=90°,∴AE=DE•cos∠DEA=2
.
在Rt△ABE中,AB=
=
=2.
(Ⅲ):过B作BO⊥AE于O点,过O作OH⊥DE于H,连BH,∵AD⊥平面ABEF,BO?面ABEF,
∴BO⊥平面ADE,∴OH为BH在平面ADE内的射影,∴BH⊥DE,即∠BHO为所求二面角的平面角.
在Rt△ABE中,BO=
. 在Rt△DBE中,由BH•DE=DB•OE得 BH=
,
∴sin∠BHO=
=
=
.
 解:(Ⅰ)证明:∵平面ABCD⊥平面ABEF,且平面ABCD∩平面ABEF=AB,
解:(Ⅰ)证明:∵平面ABCD⊥平面ABEF,且平面ABCD∩平面ABEF=AB,EB⊥AB,∴EB⊥平面ABCD,又MN∥EB,∴MN⊥面ABCD.
(Ⅱ)由(Ⅰ)可知∠EDB为DE与平面ABCD所成的角,∴∠EDB=30°.
又在Rt△EBD中,EB=2MN=2,∠EBD=90°∴DE=
| EB |
| sin30° |
连接AE,可知∠DEA为DE与平面ABEF所成的角,∴∠DEA=45°.
在Rt△DAE中,∠DAE=90°,∴AE=DE•cos∠DEA=2
| 2 |
在Rt△ABE中,AB=
| AE2-EB2 |
| 8-4 |
(Ⅲ):过B作BO⊥AE于O点,过O作OH⊥DE于H,连BH,∵AD⊥平面ABEF,BO?面ABEF,
∴BO⊥平面ADE,∴OH为BH在平面ADE内的射影,∴BH⊥DE,即∠BHO为所求二面角的平面角.
在Rt△ABE中,BO=
| 2 |
| 3 |
∴sin∠BHO=
| BO |
| BH |
| ||
|
| ||
| 3 |
点评:本题考查证明线线垂直、线面垂直的方法,求二面角的平面角的大小,找出二面角的平面角 是解题的关键.

练习册系列答案
相关题目
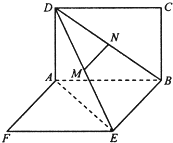 (2012•焦作模拟)如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.
(2012•焦作模拟)如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1.
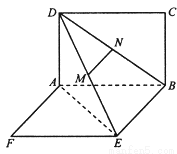
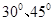 ,M、N分别为DE与DB的中点,且MN=1.
,M、N分别为DE与DB的中点,且MN=1.