题目内容
(本小题满分12分)如图,在四棱锥 中,底面ABCD为直角梯形,
中,底面ABCD为直角梯形, ,
, ,平面
,平面 ⊥底面
⊥底面 ,
, 为
为 的中点,
的中点, 是棱
是棱 上的点,
上的点, ,
, ,
,

(Ⅰ)若 是棱
是棱 的中点,求证:
的中点,求证: ;
;
(Ⅱ)求证:若二面角M-BQ-C为30°,试求 的值。
的值。
(Ⅰ)证明见解析,(Ⅱ)
【解析】
试题分析:根据线面平行的判定定理,只需寻求线线平行,由于点 是棱
是棱 的中点,可以考虑利用中位线定理,连接
的中点,可以考虑利用中位线定理,连接 交
交 于
于 ,可以证明
,可以证明 为
为 为中位线,则
为中位线,则 ,从而得出线面平行;第二步建立空间直角坐标系,写出相关点的坐标,由于平面
,从而得出线面平行;第二步建立空间直角坐标系,写出相关点的坐标,由于平面 的法向量为
的法向量为 ,再求出平面
,再求出平面 的法向量,最后利用二面角为
的法向量,最后利用二面角为 ,得出等量关系,求出
,得出等量关系,求出 的值即可.
的值即可.
试题解析:证明:(Ⅰ)连接 ,交
,交 于
于 ,连接
,连接 ,
, 且
且 ,即
,即 ,
,
∴四边形 为平行四边形,且
为平行四边形,且 为
为 中点, 又因为点
中点, 又因为点 是棱
是棱 的中点,
的中点,  ,因为
,因为  平面
平面 ,
, 平面
平面 ,则
,则 ;
;
(Ⅱ)因为 为
为 的中点, 则
的中点, 则 .∵平面
.∵平面 平面
平面 ,且平面
,且平面 平面
平面
 , ∴
, ∴ 平面
平面 ,∵
,∵ ,
, 为
为 的中点, ∴四边形
的中点, ∴四边形 为平行四边形,∴
为平行四边形,∴ , ∵
, ∵ , ∴
, ∴ ,即
,即 .
.
如图,以 为原点建立空间直角坐标系.
为原点建立空间直角坐标系.
则平面BQC的法向量为 ; 由于
; 由于 ,
, ,
, ,
,
则 ,
, ,设
,设 , 在平面
, 在平面 中,
中, ,
,
 , ∴ 平面
, ∴ 平面 法向量为
法向量为 ∵二面角
∵二面角 为
为 ,
,  ,∴
,∴  (舍), ∴
(舍), ∴
考点:1.直线与平面平行的判定定理;2.用法向量求二面角;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的定义域是( )
的定义域是( ) B、
B、 C、
C、 D、
D、
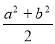 ”的 ( )
”的 ( ) 的解集为
的解集为 ,则
,则 的值是( )
的值是( ) 为等差数列,
为等差数列, 为其前
为其前 项和.若
项和.若 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 和
和 所成角大小为____________.
所成角大小为____________. 的右焦点与抛物线
的右焦点与抛物线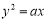 的焦点重合,则该抛物线的准线被双曲线所截的线段长度为( )
的焦点重合,则该抛物线的准线被双曲线所截的线段长度为( )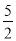 D.
D.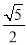
 的近似解在区间
的近似解在区间 ,则
,则 .
. ,一个等比中项是
,一个等比中项是 ,且
,且 则双曲线
则双曲线 的离子心率e等于___________;
的离子心率e等于___________;