题目内容
已知函数 (
( ,
, )在一个周期上的一系列对应值如下表:
)在一个周期上的一系列对应值如下表:
 |  |  |  |  |  |  |  |  |
 |  |  |  |  |  |  |  |  |
(Ⅰ)求
 的解析式;
的解析式;(Ⅱ)在△
 中,
中, ,
, 为锐角,且
为锐角,且 ,求△
,求△ 的面积.
的面积.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)由图象求三角函数解析式的程序是:先定振幅 ,后定周期
,后定周期 ,由周期定
,由周期定 ,最后代最高(低)点定初相
,最后代最高(低)点定初相 ;(Ⅱ)对照条件选择好面积公式,运用正弦定理即可解决问题.
;(Ⅱ)对照条件选择好面积公式,运用正弦定理即可解决问题.
试题解析:(Ⅰ)由表格知 ,从而有
,从而有 ,此时
,此时 ,将点
,将点 代入,得
代入,得 ,又
,又 ,所以有
,所以有 ,即有
,即有 .
.
(Ⅱ) ,即
,即 ,又
,又 为锐角,
为锐角,
在 中,由正弦定理得:
中,由正弦定理得:
 ,又
,又 ,
, ,
,
 .
.
考点:1.三角函数图象与性质;2.解三角形.

练习册系列答案
相关题目
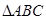 中,角
中,角 的对边分别为
的对边分别为 ,设S为△ABC的面积,满足4S=
,设S为△ABC的面积,满足4S=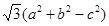 .
. 的大小;
的大小;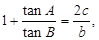 且
且 求
求 的值.
的值. 分别是角
分别是角 的对边,
的对边,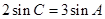 ,
,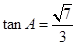 .
.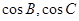 的值; (2)若
的值; (2)若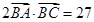 ,求
,求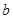 的值.
的值.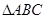 的内角
的内角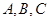 的对边分别
的对边分别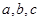 且
且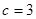 ,
,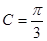 ,若
,若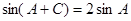 ,求
,求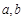 的值。
的值。
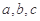 ,且,,.
,且,,.
 中,
中, 、
、 、
、 分别是
分别是 的对边,若
的对边,若 的面积为
的面积为 ,则
,则 的三个内角
的三个内角 所对的边分别为
所对的边分别为
 ,若
,若 ,
, .
.