题目内容
在锐角 中,
中, 分别是角
分别是角 的对边,
的对边,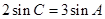 ,
,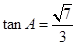 .
.
(1)求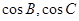 的值; (2)若
的值; (2)若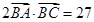 ,求
,求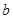 的值.
的值.
(1) ;(2)
;(2) .
.
解析试题分析:1)在三角形中,两边和一角知道,该三角形是确定的,其解是唯一的,利用余弦定理求第三边.(2)利用同角三角函数的基本关系求角的余弦值值.(3)若是已知两边和一边的对角,该三角形具有不唯一性,通常根据大边对大角进行判断.(4)在三角形中,注意 这个隐含条件的使用.(4)理解正弦定理与余弦定理的使用条件,不要搞混.
这个隐含条件的使用.(4)理解正弦定理与余弦定理的使用条件,不要搞混.
试题解析:(1)∵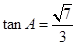 ,
, ,∵
,∵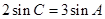 ,∴
,∴ ,
,
∴ ,∵
,∵ 是锐角三角形, ∴
是锐角三角形, ∴ ,
,
∴
 ; 6分
; 6分
(2)∵ ,∴
,∴ ;又由正弦定理
;又由正弦定理 ,得
,得 ,解得
,解得 ,
, ,∴
,∴ ,
, ,
,
即边 的长为5. 12分
的长为5. 12分
考点:(1)在三角形中求余弦值;(2)求三角形的边长.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
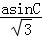 ﹣b=0.
﹣b=0.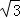 ,求bsinB+csinC的最小值.
,求bsinB+csinC的最小值. (
( ,
, )在一个周期上的一系列对应值如下表:
)在一个周期上的一系列对应值如下表:











 的解析式;
的解析式; 中,
中, ,
, 为锐角,且
为锐角,且 ,求△
,求△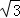 .
. acosB.
acosB.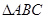 中,
中,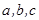 分别是角A、B、C的对边,
分别是角A、B、C的对边, 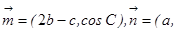
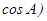 ,且
,且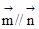 .
.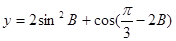 的值域.
的值域. 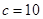 , 又知
, 又知 ,求边
,求边 、
、 的长.
的长. ,点D 在BC边上,∠ADC=45°,则AD的长度等于______。
,点D 在BC边上,∠ADC=45°,则AD的长度等于______。
 边,向量m=(
边,向量m=(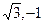 ),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=____▲_____
),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=____▲_____