题目内容
在△ABC中,若tanA∶tanB=a2∶b2,试判断△ABC的形状.
分析:可从问题已知条件出发,寻找到三角形的边与边或角与角之间的关系,然后判断.
解法一:由同角三角函数关系及正弦定理可推得![]() =
=![]() ,
,
∵A,B为三角形的内角,∴sinA≠0,sinB≠0.
∴![]() .∴sin2A=sin2B.
.∴sin2A=sin2B.
∴2A=2B或2A=π-2B.
∴A=B或A+B=![]() .
.
∴△ABC为等腰三角形或直角三角形.
解法二:由已知和正弦定理可得:
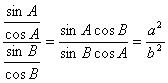 .
.
由正弦定理和余弦定理得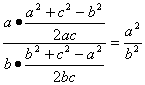 ,
,
整理得a4-a2c2+b2c2-b4=0,
即(a2-b2)(a2+b2-c2)=0.∴a2=b2或a2+b2-c2=0.∴a=b或a2+b2=c2.
∴△ABC是等腰三角形或直角三角形.
温馨提示
已知三角形中的边角关系式,判断三角形的形状,有两条思考路线:(1)化边为角,再进行三角恒等变换求出三个角之间的关系式;
(2)化角为边,再进行代数恒等变换求出三条边之间的关系式,两种转化主要应用正弦定理和余弦定理.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目