题目内容
如图△
内接于⊙O，MN切⊙O于M交AC延长线于N，且ＭＮ∥ＢＣ，ＢＣ、ＡＭ交于P, 求证：MC2=BP.MN．
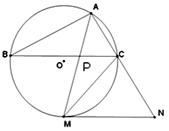
证明：∵MN是切线，∴∠CMN=∠CBM.
又ＭＮ∥ＢＣ，∠N=∠ACB
∠ACB=∠AMB ∠N= ∠AMB，∴△BPM∽△ＭＣＮ，
∴
又ＭＮ∥ＢＣ∴∠CMN=∠BCM. 又∠BCM＝∠BＡM，∠CMN＝∠MＡN
∴∠BＡM＝∠MＡN，∴ 
∴
∴MC2=BP.MN．
练习册系列答案
教材全解字词句篇系列答案
相关题目
教材全解字词句篇系列答案
A．如图，四边形ABCD内接于⊙O，弧AB=弧AD，过A点的切线交CB的延长线于E点．
（2013•牡丹江一模）选修4-1：几何证明选讲
如图所示，直线PA垂直于⊙O所在的平面，△ABC内接于⊙O，且AB为⊙O的直径，点M为线段PB的中点．现有结论：①BC⊥PC；②OM∥平面APC；③点B到平面PAC的距离等于线段BC的长．其中正确的是（ ）
=
.