Question

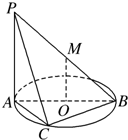如图所示，直线PA垂直于⊙O所在的平面，△ABC内接于⊙O，且AB为⊙O的直径，点M为线段PB的中点．现有结论：①BC⊥PC；②OM∥平面APC；③点B到平面PAC的距离等于线段BC的长．其中正确的是（　　）

Answer 1

分析：对于①，先根据线面垂直的判定定理证明BC⊥面PAC，然后根据线面垂直的判定定理得到结论；对于②，根据线面平行的判定定理进行判定即可；对于③，根据点到面的距离的定义进行判定即可．

解答：解：∵PA⊥圆O所在的平面，BC?圆O所在的平面，
∴PA⊥BC
而BC⊥AC，PA∩AC=A
∴BC⊥面PAC，而PC?面PAC
∴BC⊥PC，故①正确；
∵点M为线段PB的中点，点O为AB的中点
∴OM∥PA，而OM?面PAC，PA?面PAC
∴OM∥平面APC，故②正确；
∵BC⊥面PAC，∴③正确．
故选B．

点评：本题考查了线线垂直、线面垂直、线面平行的判定，考查了学生的空间想象能力与推理论证能力．