题目内容
9.直线l:y=-3x+b与圆C:(x-1)2+y2=1相交,则实数b的取值范围是(-2,8).分析 求出圆心坐标与半径,利用直线和圆相交的条件建立不等式关系进行求解即可.
解答 解:圆的标准方程为C:(x-1)2+y2=1,则圆心坐标为(1,0),半径r=1,
∵直线l:y=-3x+b与圆C:(x-1)2+y2=1相交,
∴圆心到直线的距离d=$\frac{|-3+b|}{\sqrt{9+1}}$<1,
即|b-3|<5,
则-5<b-3<5,
即-2<b<8,
故答案为:(-2,8).
点评 本题主要考查直线与圆的位置关系的应用,利用点到直线的距离与半径之间的关系是解决本题的关键.

练习册系列答案
相关题目
14.已知函数f(x)=$\frac{3{x}^{2}+ax+26}{x+1}$,若存在x∈N*使得f(x)≤2成立,则实数a的取值范围为( )
| A. | [-15,+∞) | B. | (-∞,2-12$\sqrt{2}$] | C. | (-∞,-16] | D. | (-∞,-15] |
18.为了了解汽车在某一路段上的速度,交警对这段路上连续驶过的50辆汽车的速度(单位:km/h)进行了统计,得到的数据如下表所示:
(1)试估计这段路上汽车行驶的平均速度;
(2)试估计在这段路上,汽车行驶速度的标准差.(注:为了计算方便,速度取每个区间的中点)
| 速度区间 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) | [100,110) |
| 车辆数 | 1 | 4 | 10 | 15 | 12 | 6 | 2 |
(2)试估计在这段路上,汽车行驶速度的标准差.(注:为了计算方便,速度取每个区间的中点)
 如图,在△ABC中,点D在边BC上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$
如图,在△ABC中,点D在边BC上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$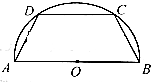 如图,有一块半径为R的半圆形钢板,计划将其剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
如图,有一块半径为R的半圆形钢板,计划将其剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.