题目内容
已知两个等比数列{an},{bn},满足a1=a(a>0),b1-a1=1,b2-a2=2,
b3-a3=3.
(1)若a=1,求数列{an}的通项公式;
(2)若数列{an}唯一,求a的值.
解析 (1)设数列{an}的公比为q,则b1=1+a=2,b2=2+aq=2+q,b3=3+aq2=3+q2,由b1,b2,b3成等比数列得(2+q)2=2(3+q2).
即q2-4q+2=0,解得q1=2+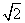 ,q2=2-
,q2=2-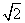 .
.
所以数列{an}的通项公式为an=(2+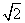 )n-1或an=(2-
)n-1或an=(2-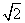 )n-1.
)n-1.
(2)设数列{an}的公比为q,则由(2+aq)2=(1+a)(3+aq2),得aq2-4aq+3a-1=0(*),
由a>0得Δ=4a2+4a>0,故方程(*)有两个不同的实根.
由数列{an}唯一,知方程(*)必有一根为0,代入(*)得a=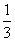 .
.

练习册系列答案
相关题目
 ≤0,
≤0, ≥0,则
≥0,则 的最小值为________.
的最小值为________.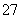 +2a11=0,数列{bn}是等比数列,且b7=a7,则b6b8=________.
+2a11=0,数列{bn}是等比数列,且b7=a7,则b6b8=________.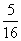 B.
B.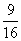 C.
C.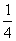 D.
D.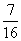
 0的等差数列,且它的第2、3、6项依次构成等比数列{ bn}的前3项。
0的等差数列,且它的第2、3、6项依次构成等比数列{ bn}的前3项。 ,当x∈
,当x∈ 时,均有
时,均有 ,则实数a的取值范围是( )
,则实数a的取值范围是( ) B.
B.
 D.
D.
 的最大值为 ( B )
的最大值为 ( B ) B.
B. C.
C. D.
D.