题目内容
已知矩阵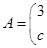
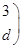，若矩阵
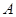属于特征值6的一个特征向量为
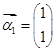，属于特征值1的一个特征向量
.
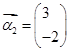（1）求矩阵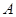的逆矩阵；
（2）计算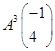
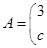
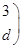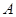，若矩阵属于特征值6的一个特征向量为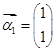，属于特征值1的一个特征向量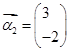.（1）求矩阵
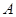的逆矩阵；（2）计算
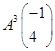
（1）
;（2）
;（2）试题分析：（1）因为已知矩阵
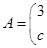
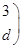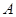，若矩阵属于特征值6的一个特征向量为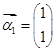，属于特征值1的一个特征向量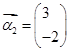.通过特征向量与特征值的关系，可求矩阵A中的相应参数的值，再通过逆矩阵的含义可求出矩阵A的逆矩阵.同样可以从通过特征根的方程方面入手，求的结论.（2）因为向量
可由向量
及向量
表示，所以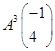即可转化为矩阵A的特征向量来表示.即可求得结论.同样也可以先求出A3，再运算即可.试题解析：(1)法一:依题意,
.
.所以
法二:
的两个根为6和1,故d=4,c=2.
所以-(2)法一:
=2
－
A3
=2×63－13=
法二:
A3
=
练习册系列答案
相关题目
，
，计算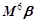
．
，若点P(1，1)在矩阵A对应的变换作用下得到点P′(0，-8)．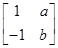
，A的一个特征值λ＝2，其对应的特征向量是α1＝
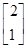.设向量β＝
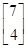，试计算A5β的值．
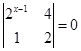，则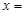
.
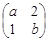有一个属于特征值1的特征向量
.
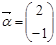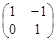，点O(0,0)，M(2，-1)，N(0，2)，求
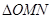在矩阵AB的对应变换作用下所得到的
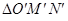的面积. 
对应变换的作用下得到的点为B(－1,1)，求矩阵M的逆矩阵．
,B=
,C=
,求AB和AC.