题目内容
函数f（x）=2x-lnx的单调增区间是________．
（
，+∞）
分析：求出f′（x），在定义域内解不等式f′（x）＞0即得单调增区间．
解答：f（x））=2x-lnx的定义域为（0，+∞）．
f′（x）=2-
=
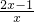，令f′（x）＞0，解得x
．
所以函数f（x）=2x-lnx的单调增区间是（，+∞）．
故答案为：（，+∞）．
点评：本题考查运用导数研究函数的单调性，注意考函数虑定义域．
，+∞）分析：求出f′（x），在定义域内解不等式f′（x）＞0即得单调增区间．
解答：f（x））=2x-lnx的定义域为（0，+∞）．
f′（x）=2-
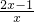=，令f′（x）＞0，解得x．所以函数f（x）=2x-lnx的单调增区间是（
，+∞）．故答案为：（
，+∞）．点评：本题考查运用导数研究函数的单调性，注意考函数虑定义域．
练习册系列答案
相关题目
设函数f（x）=
，则满足f（x）=4的x的值是（ ）
|
| A、2 | B、16 |
| C、2或16 | D、-2或16 |