题目内容
已知正项数列 的前项和为
的前项和为 ,且满足
,且满足
(1)求数列 的通项公式;(2)设
的通项公式;(2)设 ,则是否存在数列
,则是否存在数列 ,满足
,满足 对一切正整数
对一切正整数 都成立?若存在,请求出数列
都成立?若存在,请求出数列 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
【答案】
解:(1)当 时,
时,
 ,故
,故 。---------(2分)
。---------(2分)
当 时,
时, ,两式相减得到
,两式相减得到 ,所以数列
,所以数列 为首项为
为首项为 ,公比为
,公比为 的等比数列,所以
的等比数列,所以 ----------(7分)
----------(7分)
(2)因为 ,所以
,所以 ,若存在满足题意的数列
,若存在满足题意的数列 ,
,
则 ,
,
两式相减,得到 ------------(12分)
------------(12分)
由 ,得到
,得到 ,满足上式。所以,存在满足题意的数列
,满足上式。所以,存在满足题意的数列 ,通项公式为
,通项公式为 ---------------(14分)
---------------(14分)
【解析】略

练习册系列答案
相关题目
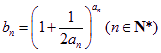 .
.
 的前
的前 项和
项和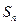 满足:
满足: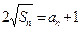 ;设
;设 ,求数列
,求数列 的前
的前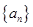 的前
的前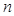 项和为
项和为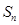 ,且
,且
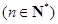 .
.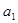 的值及数列
的值及数列
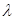 ,使不等式
,使不等式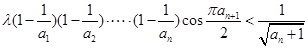
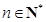 都成立?若存在,求出
都成立?若存在,求出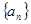 的前
的前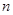 项和为
项和为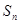 ,且满足
,且满足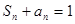 .
.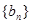 满足
满足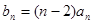 ,且数列
,且数列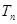 ,
,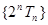 为等差数列.
为等差数列.