题目内容
已知正项数列![]() 的前
的前![]() 项和
项和![]() ,
,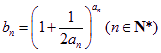 .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)定理:若函数![]() 在区间D上是凹函数,且
在区间D上是凹函数,且![]() 存在,则当
存在,则当![]() 时,总有
时,总有![]() .请根据上述定理,且已知函数
.请根据上述定理,且已知函数![]() 是
是![]() 上的凹函数,判断
上的凹函数,判断![]() 与
与![]() 的大小;
的大小;
(Ⅲ)求证:![]() .
.
(Ⅰ)![]() (
(![]() ).
).
(Ⅱ)![]() .
.
(Ⅲ)由(Ⅱ),得![]() .
.
解析:
(Ⅰ)![]() 时,
时,![]() 或
或![]() .
.
由于![]() 是正项数列,所以
是正项数列,所以![]() .
.
当![]() 时,
时,
![]() ,
,
整理,得![]() .
.
由于![]() 是正项数列,∴
是正项数列,∴![]() .
.
∴数列![]() 是以1为首项,1为公差的等差数列.
是以1为首项,1为公差的等差数列.
从而![]() ,当
,当![]() 时也满足.
时也满足.
∴![]() (
(![]() ).
).
(Ⅱ)由(Ⅰ)知 .
.
对于![]() 上的凹函数
上的凹函数![]() ,有
,有![]() .
.
根据定理,得![]() .
.
整理,得![]() .
.
令![]() ,得
,得![]() .
.
∴![]() ,即
,即 .
.
∴![]() .
.
(Ⅲ)由(Ⅱ),得![]() .
.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目

 的前
的前 项和
项和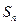 满足:
满足: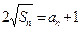 ;设
;设 ,求数列
,求数列 的前
的前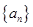 的前
的前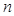 项和为
项和为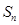 ,且
,且
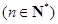 .
.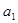 的值及数列
的值及数列
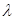 ,使不等式
,使不等式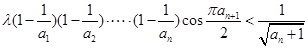
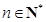 都成立?若存在,求出
都成立?若存在,求出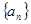 的前
的前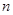 项和为
项和为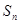 ,且满足
,且满足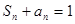 .
.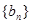 满足
满足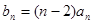 ,且数列
,且数列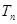 ,
,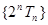 为等差数列.
为等差数列.