题目内容
(满分12分)
已知正项数列
 的前
的前 项和
项和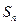 满足:
满足: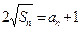 ;设
;设 ,求数列
,求数列 的前
的前 项和的最大值。
项和的最大值。

当 时
时 最大,最大值为
最大,最大值为
解析解:当 时,
时, ,所以
,所以 ,即
,即 ,∴
,∴ ;
; ……1分
……1分
当 时,由
时,由 ,得
,得 ……①, www.k@s@5@u.com 高#考#资#源#网
……①, www.k@s@5@u.com 高#考#资#源#网
∴ ……② 两式相减,得
……② 两式相减,得
整理,得 ,…………6分
,…………6分
∵ ,∴
,∴ , ∴
, ∴ ,
,
∴ 是以1为首项,以2为公差的等差数列,
是以1为首项,以2为公差的等差数列, …………8分
…………8分
∴ ,∴
,∴ ,
,
∴ ,又
,又
∴ 是等差数列,且
是等差数列,且 ,公差
,公差 ,
,
∴ ,…………10分
,…………10分
∴当 时,
时, 取最大值,但
取最大值,但
 ,…………11分
,…………11分
∴当 时
时 最大,最大值为
最大,最大值为 。…………12分
。…………12分

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 的前
的前 项和为
项和为 ,若
,若 ,且
,且 成等比数列.
成等比数列. 的前
的前 ,求证
,求证 .
. 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, .
. ;
; 满足
满足 且
且 ,求数列
,求数列 的前
的前 .
.
 ,高为
,高为 ,
,
 的前
的前 项和
项和 满足:
满足: ;设
;设 ,求数列
,求数列 的前
的前 中,
中, ,点
,点 在函数
在函数 的图像上,数列
的图像上,数列 中,点
中,点 在直线
在直线 上,其中
上,其中 是数列
是数列 。
。