题目内容
4.已知向量$\overrightarrow{AB}$,$\overrightarrow{AC}$夹角为120°,|$\overrightarrow{AB}$|=5,|$\overrightarrow{AC}$|=2,$\overrightarrow{AP}$=$\overrightarrow{AB}$+λ$\overrightarrow{AC}$,若$\overrightarrow{AP}$⊥$\overrightarrow{BC}$,则λ=$\frac{10}{3}$.分析 根据向量数量积的公式,结合向量垂直的关系即可得到结论.
解答 解:∵向量$\overrightarrow{AB}$,$\overrightarrow{AC}$夹角为120°,|$\overrightarrow{AB}$|=5,|$\overrightarrow{AC}$|=2,
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos120°=5×2×(-$\frac{1}{2}$)=-5,
∵$\overrightarrow{AP}$=$\overrightarrow{AB}$+λ$\overrightarrow{AC}$,$\overrightarrow{AP}$⊥$\overrightarrow{BC}$,
∴($\overrightarrow{AB}$+λ$\overrightarrow{AC}$)•$\overrightarrow{BC}$=($\overrightarrow{AB}$+λ$\overrightarrow{AC}$)($\overrightarrow{AC}$-$\overrightarrow{AB}$)=0,
即$\overrightarrow{AB}•\overrightarrow{AC}$-${\overrightarrow{AB}}^{2}$+λ${\overrightarrow{AC}}^{2}$-λ$\overrightarrow{AC}•\overrightarrow{AB}$=0,
∴-5-25+4λ+5λ=0
解得λ=$\frac{10}{3}$,
故答案为:$\frac{10}{3}$.
点评 本题主要考查平面向量的基本运算,利用向量垂直和数量积之间的关系是解决本题的关键.

| A. | (0,2) | B. | (0,4] | C. | [-2,0) | D. | [-4,0) |
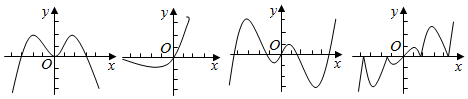
| A. | ①④③② | B. | ①④②③ | C. | ④①②③ | D. | ③④②① |
| A. | $\sqrt{13}$ | B. | 4 | C. | 3 | D. | $\sqrt{15}$ |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
| A. | $\frac{2π}{5}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{5}$ | D. | $\frac{π}{3}$ |