题目内容
已知圆M的方程为x2+y2-2x-3=0,求圆心M的坐标.
考点:圆的一般方程
专题:直线与圆
分析:把圆的一般方程化为标准方程,可得它的圆心坐标.
解答:
解:圆M的方程为x2+y2-2x-3=0,即圆M的方程为(x-1)2+y2 =4,
故它的圆心为M(1,0).
故它的圆心为M(1,0).
点评:本题主要考查圆的一般方程的特征,属于基础题.

练习册系列答案
相关题目
设x=
+2
,y=3-
,集合M={m|m=a+b
,a∈Q,b∈Q},那么x,y与集合M的关系是( )
| 1 |
| 3 |
| 2 |
| 2 |
| 2 |
| A、x∈M y∈M |
| B、x∈M y∉M |
| C、x∉M y∈M |
| D、x∉M y∉M |
设f(x)是R上的偶函数,且在[0,+∞)上是增函数,又f(1)=0,则满足f(log2x)>0的x的取值范围是( )
| A、(2,+∞) | ||
B、(0,
| ||
C、(0,
| ||
D、(
|
设
为复数z=
-i的共轭复数,(z-
)2014=( )
. |
| z |
| 1 |
| 2 |
. |
| z |
| A、22014 |
| B、-22014 |
| C、22014i |
| D、-i |
在(
+
)12的展开式中,x项的系数为( )
| x |
| 1 | |||
|
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
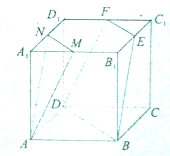 棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.
棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.