Question

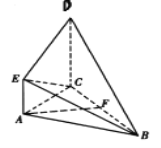
【题目】如图，已知正方形ABCD和矩形ACEF所在平面相互垂直，AB= ，AF=1，G为线段AD上的任意一点．
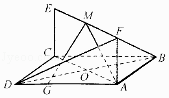
（1）若M是线段EF的中点，证明：平面AMG⊥平面BDF；
（2）若N为线段EF上任意一点，设直线AN与平面ABF，平面BDF所成角分别是α，β，求 的取值范围．

Answer 1

【答案】
（1）证明：设AC∩BD=O，连结OF，OM，

由已知得AO=1，AF=1，

∴四边形AFMO是正方形，∴AM⊥OF，

又∵正方形ABCD和矩形ACEF所在平面互相垂直，交线是CA，DB⊥CA，

∴DB⊥平面ACEF，又AM平面ACEF，∴DB⊥AM，

∵BD∩OF=O，∴AM⊥平面BDF，

∵AM平面AMG，∴平面AMG⊥平面BDF

（2）解：∵正方形ABCD和矩形ACEF所在平面互相垂直，交线是CA，EC⊥CA，

∴EC⊥平面ABCD，∴CD、CB、CE两两垂直，

分别以CD、CB、CE为x，y，z轴建立坐标系，

则平面ABF的法向量 =（0，1，0），

由（1）得平面BDF的法向量 = =（﹣ ，﹣ ，1），

由N为线段EF上任意一点，

设 = = =λ（ ），（λ∈[0，1]），

∴ =（（λ﹣1） ，（λ﹣1） ，1），

∴sinα= = = ，

∵λ∈[0，1]，∴ = =1﹣ ∈[0， ]．

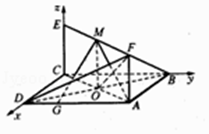
【解析】（1）设AC∩BD=O，连结OF，OM，推导出AM⊥OF，DB⊥CA，从而DB⊥平面ACEF，进而DB⊥AM，AM⊥平面BDF，由此能证明平面AMG⊥平面BDF．（2）分别以CD、CB、CE为x，y，z轴建立坐标系，利用向量法能求出 的取值范围．
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案，需要熟知一个平面过另一个平面的垂线，则这两个平面垂直．