题目内容
给定椭圆C: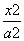 +
+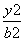 =1(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为
=1(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为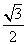 ,且经过点(0,1).
,且经过点(0,1).
(1)求实数a,b的值;
(2)若过点P(0,m)(m>0)的直线l与椭圆C有且只有一个公共点,且l被椭圆C的伴随圆C1所截得的弦长为2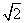 ,求实数m的值.
,求实数m的值.
解:(1)记椭圆C的半焦距为c.
由题意,得b=1,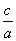 =
=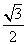 ,c2=a2+b2,
,c2=a2+b2,
解得a=2,b=1.
(2)由(1)知,椭圆C的方程为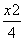 +y2=1,圆C1的方程为x2+y2=5.
+y2=1,圆C1的方程为x2+y2=5.
显然直线l的斜率存在.
设直线l的方程为y=kx+m,即kx-y+m=0.
因为直线l与椭圆C有且只有一个公共点,
故方程组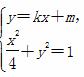 (*) 有且只有一组解.
(*) 有且只有一组解.
由(*)得(1+4k2)x2+8kmx+4m2-4=0.
从而△=(8km)2-4(1+4k2)( 4m2-4)=0.
化简,得m2=1+4k2.①
因为直线l被圆x2+y2=5所截得的弦长为2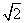 ,
,
所以圆心到直线l的距离d=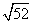 =
=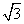 .
.
即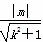 =
=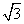 . ②
. ②
由①②,解得k2=2,m2=9.
因为m>0,所以m=3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的最小值为________.
的最小值为________.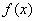 满足
满足 ,且对任意
,且对任意 都有
都有 ,则不等式
,则不等式 的解集为( )
的解集为( ) D.(-1,1)
D.(-1,1)
 +
+ |的最大值是 .
|的最大值是 .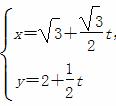 (t为参数 ),圆C的参数方程为
(t为参数 ),圆C的参数方程为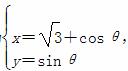 (θ为参数).若点P是圆C上的动点,求点P到直线l的距离的最小值.
(θ为参数).若点P是圆C上的动点,求点P到直线l的距离的最小值. β,则l∥m.
β,则l∥m. .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程; 时,设函数
时,设函数 ,若对于
,若对于 ,
, ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.