题目内容
在平面直角坐标系xOy中,已知直线l的参数方程为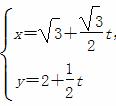 (t为参数 ),圆C的参数方程为
(t为参数 ),圆C的参数方程为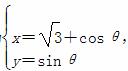 (θ为参数).若点P是圆C上的动点,求点P到直线l的距离的最小值.
(θ为参数).若点P是圆C上的动点,求点P到直线l的距离的最小值.
解:(方法一)
直线l的普通方程为x-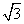 y+
y+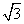 =0.
=0.
因为点P在圆C上,故设P(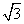 +cosθ,sinθ),
+cosθ,sinθ),
从而点P到直线l的距离
d=
所以dmin=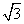 -1.
-1.
即点P到直线l的距离的最小值为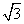 -1.
-1.
(方法二)
直线l的普通方程为x-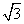 y+
y+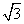 =0.
=0.
圆C的圆心坐标为(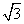 ,0),半径为1.
,0),半径为1.
从而圆心C到直线l的距离为d= =
=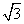 . …
. …
所以点P到直线l的距离的最小值为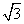 -1.
-1.

练习册系列答案
相关题目

 都有
都有 成立,求
成立,求 的取值范围;(6分)
的取值范围;(6分) 都有
都有 成立,求
成立,求 上的奇函数
上的奇函数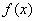 在
在 时满足
时满足 ,且
,且 在
在 恒成立,则实数
恒成立,则实数 的最大值是 .
的最大值是 . 是R上的单调函数,则实数a的取值范围为 .
是R上的单调函数,则实数a的取值范围为 .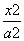 +
+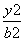 =1(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为
=1(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为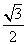 ,且经过点(0,1).
,且经过点(0,1).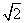 ,求实数m的值.
,求实数m的值. 满足
满足 ,则
,则 B.
B. C.
C. D.
D.
 <cos A,则△ABC为
<cos A,则△ABC为 (其中
(其中 为虚数单位),则
为虚数单位),则 的虚部为( )
的虚部为( ) B、
B、 C、
C、 D、
D、