题目内容
20．若在区间[-1，5]上任取一个数b，则函数f（x）=x-blnx（x＞3）在定义域上是单调函数的概率为$\frac{2}{3}$．分析 由题意，本题属于几何概型的概率求法，由此只要求出所有事件的区域长度以及满足条件的b的范围对应的区域长度，利用几何概型概率公式可求．
解答 解：∵f（x）=x-blnx，
∴f′（x）=1-$\frac{b}{x}$≥0，可得b≤x，
∵x＞3，∴b≤3，
∴在区间[-1，5]上任取一个数b，函数f（x）=x-blnx（x＞3）在定义域上是单调函数的概率为$\frac{3+1}{5+1}$=$\frac{2}{3}$，
故答案为$\frac{2}{3}$．
点评 本题主要考查几何概型，考查利用导数研究函数的单调性，正确把握导数的正负与函数单调性之间的关系是关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
11．在△ABC中，角A、B、C所对的边分别是a、b、c，若a=2，A=$\frac{π}{6}$，则△ABC外接圆的面积等于（ ）
| A． | $\frac{π}{4}$ | B． | π | C． | 4π | D． | 16π |
15．下列函数中最小正周期为π且为偶函数的是（ ）
| A． | $y=cos（2x-\frac{π}{2}）$ | B． | $y=sin（2x+\frac{π}{2}）$ | C． | $y=sin（x+\frac{π}{2}）$ | D． | $y=cos（x-\frac{π}{2}）$ |
5．
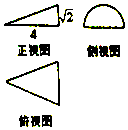一个几何体的三视图及尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，该几何体的体积为（ ）
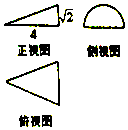一个几何体的三视图及尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，该几何体的体积为（ ）| A． | $\frac{4}{3}$π | B． | $\frac{4\sqrt{2}}{3}$π | C． | 4π | D． | 4$\sqrt{2}$π |
12．设集合A={x|x2-1＜0}，B={y|y=2x，x∈A}，则A∩B=（ ）
| A． | （0，1） | B． | （-1，2） | C． | （-1，+∞） | D． | $（\frac{1}{2}，1）$ |