题目内容
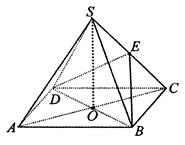
(本题满分12分)如图,四棱锥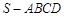 中,底面
中,底面 是边长为4的正方形,
是边长为4的正方形,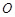 是
是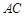 与
与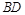 的交点,
的交点,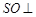 平面
平面 ,
,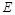 是侧棱
是侧棱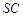 的中点,异面直线
的中点,异面直线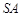 和
和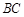 所成角的大小是60
所成角的大小是60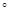 .
.
(Ⅰ)求证:直线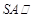 平面
平面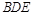 ;
;
(Ⅱ)求直线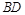 与平面
与平面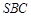 所成角的正弦值.
所成角的正弦值.
(Ⅰ)见解析;(Ⅱ)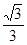 。
。
解析试题分析:(Ⅰ)连结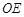 ,……1分
,……1分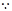 四边形
四边形 是正方形,
是正方形, 是
是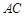 的中点,…2分
的中点,…2分
又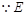 是侧棱
是侧棱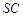 的中点,
的中点,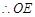 //
//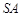 .又
.又 平面
平面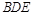 ,
, 平面
平面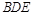 ,
,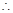 直线
直线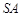 //平面
//平面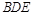 .…………4分
.…………4分
(Ⅱ)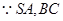 所成角为
所成角为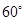 ,
,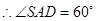 ,
,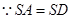
 为等边三角形
为等边三角形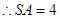 ......5分在
......5分在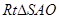 中,
中,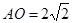 ,
,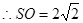 建立如图空间坐标系,
建立如图空间坐标系,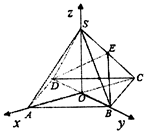
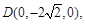
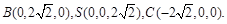
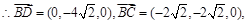
 …………………7分
…………………7分
设平面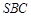 的法向量
的法向量 ,则有
,则有 即
即 解得
解得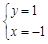
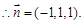 …………9分
…………9分
直线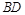 与平面
与平面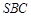 所成角记为
所成角记为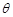 ,则
,则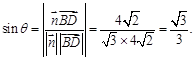 …12分
…12分
考点:线面垂直的性质定理;异面直线所成的角;直线与平面所成的角;直线与平面平行的判定定理.
点评:本题考查直线与平面平行的证明及直线与平面所成角的正弦值的求法.解题时要认真审题,仔细解答,注意向量法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
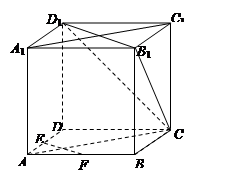
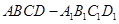 是正方体,其中
是正方体,其中
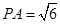
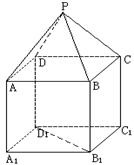
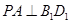 ;
;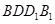 所成的锐二面角
所成的锐二面角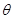 的余弦值;
的余弦值;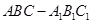 中,
中,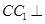 平面
平面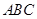 ,
,  ,点
,点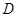 是
是 的中点.
的中点.
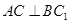 ;(2)
;(2)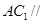 平面
平面 .
.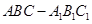 的侧面
的侧面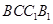 是菱形,
是菱形,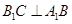
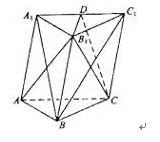
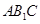
 平面
平面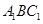 ;
; 是
是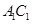 上的点,且
上的点,且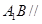 平面
平面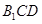 ,求
,求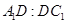 的值.
的值.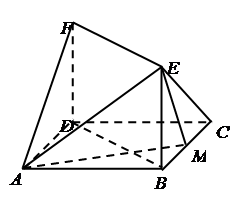
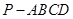 中,
中,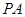 ⊥底面
⊥底面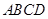 ,底面
,底面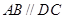 ,
,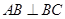 ,
,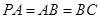 ,点
,点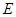 在棱
在棱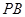 上,且
上,且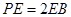 .
.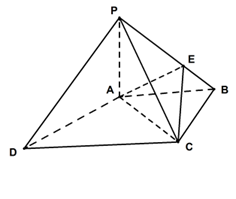
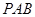 ⊥平面
⊥平面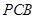 ;
;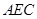 和平面
和平面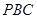 所成锐二面角的余弦值.
所成锐二面角的余弦值.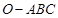 的侧棱
的侧棱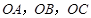 两两垂直,
两两垂直,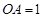 ,
, ,
,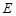 是
是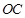 的中点。
的中点。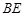 与
与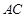 所成角的余弦值;
所成角的余弦值;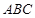 的所成角的正弦值。
的所成角的正弦值。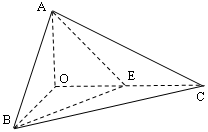
 和直线
和直线 ,给出条件:
,给出条件: ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .
. ;
;