题目内容
5.已知△ABC的三个内角A,B,C所对的边分别为a,b,c,asinC=csinB.(Ⅰ)判断△ABC的形状;
(Ⅱ)若B=30°,a=2,求BC边上中线AD的长.
分析 (Ⅰ)由已知等式,利用正弦定理可得:ac=cb,解得:a=b,即可得解△ABC为等腰三角形.
(Ⅱ)由已知可求C=120°,BD=1,利用余弦定理可求AB,在△ABD中,利用余弦定理可求AD的值.
解答 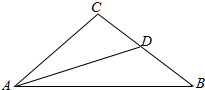 解:(Ⅰ)∵asinC=csinB.
解:(Ⅰ)∵asinC=csinB.
∴利用正弦定理可得:ac=cb,解得:a=b,
∴△ABC为等腰三角形.
(Ⅱ)如图所示:∵BC=AC,B=30°,BC=2,
∴C=120°,BD=1,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}-2•AC•BC•cosC}$=$\sqrt{4+4-2×2×2×(-\frac{1}{2})}$=2$\sqrt{3}$,
∴△ABD中,AD=$\sqrt{A{B}^{2}+B{D}^{2}-2•AB•BD•cosB}$=$\sqrt{12+1-2×2\sqrt{3}×1×\frac{\sqrt{3}}{2}}$=$\sqrt{7}$.
点评 本题主要考查了正弦定理,余弦定理,三角形内角和定理的综合应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
15.已知椭圆$\frac{x^2}{2}$+y2=1与直线y=x+m交于A、B两点,且|AB|=$\frac{4\sqrt{2}}{3}$,则实数m的值为( )
| A. | ±1 | B. | ±$\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | ±$\sqrt{2}$ |
13.设集合A={x|x2-2x≥0},集合B={x|2x>1},则A∩B=( )
| A. | (0,2] | B. | [0,2] | C. | [2,+∞) | D. | (2,+∞) |
20.已知抛物线x2=8y上的点P到抛物线的焦点距离为5,则点P的纵坐标为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
14.执行如图所示的程序框图,若m=3,则输出的结果为( )
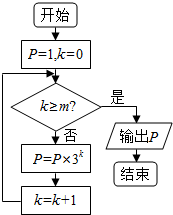

| A. | 3 | B. | 27 | C. | 81 | D. | 729 |
