题目内容
【题目】已知锐角△ABC的三个内角A，B，C的对边分别为a，b，c，且 
=（a，b+c）， 
．
（1）求角A；
（2）若a=3，求△ABC面积的取值范围．
【答案】
（1）解：由 
，得 
由正弦定理得 
因为B=π﹣A﹣C
所以 
所以 
由于sinC≠0，所以 
由 
，得 
，故 
.
（2）解：由 
，得 
，
所以 
= 
由△ABC为锐角三角形，所以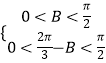 
，得 
，
所以 
， 
，
故6＜bc≤9，
又 
，
所以，△ABC面积的取值范围为 
．
【解析】（1）由 ，结合正弦定理，通过B=π﹣A﹣C，化简表达式利用两角和与差的三角函数推出 锐角求解A．（2）利用正弦定理以及两角和与差的三角函数，结合B的范围，求解三角形的面积的范围即可．
练习册系列答案
相关题目
