题目内容

【题目】如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，点P是平面A1BC1内一动点，且满足|PD|+|PB1|=6，则点P的轨迹所形成的图形的面积是（ ）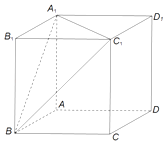
A.2π
B.
C.
D.

【答案】D
【解析】解：连接B1D，记B1D与平面A1BC1交于点O，易证B1D⊥平面A1BC1 ， 丨OD丨=2丨OB1丨= ．由|PD|+|PB1|=6＞丨B1D丨=2 ， 点P在一个“椭球”上运动，且被垂直于其对称轴的平面A1BC1截出一个圆，记其半径为r，记丨PD丨=a，
则 ，解得 ，
所以点P的轨迹所形成的图形的面积S=πr2= ，
故选D．

【考点精析】本题主要考查了棱柱的结构特征的相关知识点，需要掌握两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形才能正确解答此题．

练习册系列答案
相关题目

【题目】如图，正方体AC1的棱长为1，过点A作平面A1BD的垂线，垂足为点H，则以下命题中，错误的命题是（ ）

A.点H是△A1BD的垂心
B.AH垂直平面CB1D1
C.AH的延长线经过点C1
D.直线AH和BB1所成角为45°

【题目】已知函数f（x）= 为偶函数．
（1）求实数a的值；
（2）记集合E={y|y=f（x），x∈{﹣1，1，2}}，λ=（lg 2）2+lg 2lg 5+lg 5﹣ ，判断λ与E的关系；
（3）当x∈[ ， ]（m＞0，n＞0）时，若函数f（x）的值域为[2﹣3m，2﹣3n]，求m，n的值．

【题目】根据所给条件求直线的方程：
（1）直线过点（﹣4，0），倾斜角的正弦值为 ；
（2）直线过点（﹣2，1），且到原点的距离为2．

【题目】已知△ABC的三个顶点A（4，﹣6），B（﹣4，0），C（﹣1，4），求：
（1）BC边的垂直平分线EF的方程；
（2）AB边的中线的方程．

【题目】在平面四边形ABCD中，AB=BD=CD=1，AB⊥BD，CD⊥BD，将△ABD沿BD折起，使得平面ABD⊥平面BCD，如图．

（1）求证：AB⊥CD；
（2）若M为AD中点，求直线AD与平面MBC所成角的正弦值．

【题目】已知函数.

讨论函数的单调性；

设函数的最小值为，且关于的方程恰有两个不同的根，求实数的取值集合.

【题目】已知锐角△ABC的三个内角A，B，C的对边分别为a，b，c，且 =（a，b+c）， ．
（1）求角A；
（2）若a=3，求△ABC面积的取值范围．

【题目】如图所示，在四棱锥P﹣ABCD中，底面ABCD是边长为2的正方形，其它四个侧面都是侧棱长为 的等腰三角形．
（Ⅰ）求二面角P﹣AB﹣C的大小；
（Ⅱ）在线段AB上是否存在一点E，使平面PCE⊥平面PCD？若存在，请指出点E的位置并证明，若不存在请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网