题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}{x+1,-1<x<0}\\{{x}^{2},0≤x≤5}\end{array}\right.$,则f(x)的定义域是{x|-1<x≤5}.分析 根据分段函数的定义域是各段函数的定义域的并集,求出即可.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{x+1,-1<x<0}\\{{x}^{2},0≤x≤5}\end{array}\right.$,
∴f(x)的定义域为
{x|-1<x<0}∪{x|0≤x≤5}={x|-1<x≤5}.
故答案为:{x|-1<x≤5}.
点评 本题考查了分段函数的定义域的应用问题,是基础题目.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
14.有红、蓝颜色的旗帜各两面,在每种颜色的旗帜上分别标有号码1、2,从中任取两面,假设每面旗帜被取到的可能性相等,则取出的两面旗帜的颜色和号码均不相同的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
11.若a≥0,b≥0,且当$\left\{\begin{array}{l}{|x|≤1}\\{|y|≤1}\end{array}\right.$时,恒有2ax+by≤1,则点P(a+b,a-b)所形成的平面区域的面积是( )
| A. | $\frac{π}{2}$ | B. | 2π | C. | 1 | D. | $\frac{1}{2}$ |
18.已知直线l经过点A(1,-2),B(-3,2),则直线l的方程是( )
| A. | x+y+1=0 | B. | x-y+1=0 | C. | x+2y+1=0 | D. | x+2y-1=0 |
4.已知f(x)是定义在R上的不恒等于0的偶函数,且对于任意实数x都有xf(x+1)=(x+1)f(x),则$f(\frac{9}{2})$的值为( )
| A. | 1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{9}{2}$ |
11.若△ABC的三边为a,b,c,它的面积为$\frac{1}{4}$(a2+b2-c2),那么内角C等于( )
| A. | 30° | B. | 90° | C. | 60° | D. | 45° |
9.某地区人民法院每年要审理大量案件,去年审理的四类案件情况如表所示:
其中结案包括:法庭调解案件、撤诉案件、判决案件等.根据以上数据,回答下列问题.
(Ⅰ)在编号为1、2、3的收案案件中随机取1件,求该件是结案案件的概率;
(Ⅱ)在编号为2的结案案件中随机取1件,求该件是判决案件的概率;
(Ⅲ)在编号为1、2、3的三类案件中,判决案件数的平均数为$\overline x$,方差为S12,如果表中n=$\overline x$,表中全部(4类)案件的判决案件数的方差为S22,试判断S12与S22的大小关系,并写出你的结论(结论不要求证明).
| 编号 | 项目 | 收案(件) | 结案(件) | |
| 判决(件) | ||||
| 1 | 刑事案件 | 2400 | 2400 | 2400 |
| 2 | 婚姻家庭、继承纠纷案件 | 3000 | 2900 | 1200 |
| 3 | 权属、侵权纠纷案件 | 4100 | 4000 | 2000 |
| 4 | 合同纠纷案件 | 14000 | 13000 | n |
(Ⅰ)在编号为1、2、3的收案案件中随机取1件,求该件是结案案件的概率;
(Ⅱ)在编号为2的结案案件中随机取1件,求该件是判决案件的概率;
(Ⅲ)在编号为1、2、3的三类案件中,判决案件数的平均数为$\overline x$,方差为S12,如果表中n=$\overline x$,表中全部(4类)案件的判决案件数的方差为S22,试判断S12与S22的大小关系,并写出你的结论(结论不要求证明).
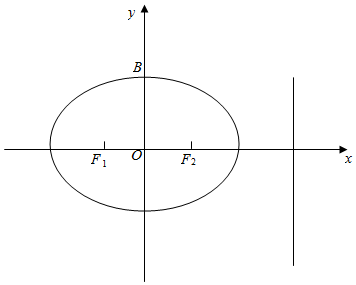 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点B(0,$\sqrt{3}$)是椭圆E的上顶点,F1,F2分别是椭圆E的左、右焦点.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点B(0,$\sqrt{3}$)是椭圆E的上顶点,F1,F2分别是椭圆E的左、右焦点.