题目内容
5.已知椭圆E的中心为坐标原点,关于坐标轴对称,经过点$M(1,\frac{{\sqrt{6}}}{2})$和$N(\sqrt{2},1)$.A、B为椭圆的左右顶点,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.(1)求椭圆E的方程;
(2)求证:直线PQ过定点,并求定点坐标.
分析 (1)设椭圆的方程,代入椭圆方程,即可求得m和n的值,求得椭圆的方程;
(2)设P点坐标,根据直线的斜率公式求得kBP•kBQ=-1,设直线PQ的方程,代入椭圆方程,利用韦达定理及向量数量积的坐标运算,即可求得b=-$\frac{2}{3}$k,即可求得直线恒过定点.
解答 解:(1)设椭圆的方程为:mx2+ny2=1,(m>0,n>0),
则$\left\{\begin{array}{l}{m+\frac{3}{2}n=1}\\{2m+n=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=\frac{1}{4}}\\{n=\frac{1}{2}}\end{array}\right.$,
∴椭圆的标准方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$;
(2)证明:设P点坐标(x,y),y2=$\frac{1}{2}$(4-x2),则A(-2,0),B(2,0),则
kAP=$\frac{y-0}{x+2}$,kBP=$\frac{y-0}{x-2}$,
则kAP•kBP=$\frac{{y}^{2}}{{x}^{2}-4}$=-$\frac{1}{2}$,
由kBQ=2kAP,故kBP•kBQ=-1.
∴直线BP与直线BQ的斜率乘积为-1为定值,
当直线PQ的斜率存在时,设lPQ:y=kx+b与x轴的交点为M,
$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\\{y=kx+b}\end{array}\right.$,整理得:(2k2+1)x2+4kbx+2b2-4=0,
设P(x1,y1),Q(x2,y2),则x1+x2=-$\frac{4kb}{2{k}^{2}+1}$,x1x2=$\frac{2{b}^{2}-4}{2{k}^{2}+1}$,
由kBP•kBQ=-1,即$\overrightarrow{BP}$•$\overrightarrow{BQ}$=0,则y1y2+x1x2-2(x1+x2)+4=0,
得(k2+1)x1x2+(kb-2)(x1+x2)+4+b2=0,
4k2+8kb+3b2=0,得b=-2k或b=-$\frac{2}{3}$k.y=k(x-2)或y=k(x-$\frac{2}{3}$),
所以过定点(2,0)或($\frac{2}{3}$,0),
A(2,0)为椭圆的右顶点,舍去,
∴直线PQ过定点($\frac{2}{3}$,0).
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | (-1,1) | B. | [-1,1] | C. | (-∞,1] | D. | [1,+∞) |
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 的图象向右平移
的图象向右平移 个单位后得到函数
个单位后得到函数 的图象,若函数
的图象,若函数 和
和 上均单调递增,则实数
上均单调递增,则实数 的取值范围是 ( )
的取值范围是 ( )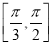 B.
B. C.
C. D.
D.
 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,且满足
,且满足 .
. 的大小;
的大小; ,求角
,求角 的大小.
的大小. 的抛物线的标准方程为 .
的抛物线的标准方程为 . 如图,在边长为1的正方体中ABCD-A1B1C1D1,P、Q分别是线段BD、C1C上的动点,则|PQ|的最小值是$\frac{\sqrt{2}}{2}$.
如图,在边长为1的正方体中ABCD-A1B1C1D1,P、Q分别是线段BD、C1C上的动点,则|PQ|的最小值是$\frac{\sqrt{2}}{2}$.