题目内容
设变量x、y满足约束条件
且不等式x+2y≤14恒成立，则实数a的取值范围是 ．
|
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，利用目标函数的几何意义，进行求最值即可．
解答：
解：不等式组表示的平面区域如图中阴影部分所示，显然a≥8，否则可行域无意义．
由图可知x+2y在点（6，a-6）处取得最大值2a-6，
由2a-6≤14得，a≤10，
故8≤a≤10，
故答案为：8≤a≤10．
解：不等式组表示的平面区域如图中阴影部分所示，显然a≥8，否则可行域无意义．由图可知x+2y在点（6，a-6）处取得最大值2a-6，
由2a-6≤14得，a≤10，
故8≤a≤10，
故答案为：8≤a≤10．
点评：本题主要考查线性规划的基本应用，利用目标函数的几何意义是解决问题的关键，利用数形结合是解决问题的基本方法．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
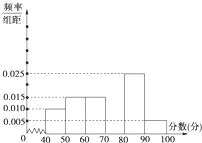某中学团委组织了“弘扬奥运精神，爱我中华”的知识竞赛，从参加考试的学生中抽出60名学生，将其成绩（均为整数）分成六段[40，50），[50，60），…，[90，100]后画出如图所示部分频率分布直方图．观察图形给出的信息，回答下列问题：