Question

斜率为

4

3

的直线l经过抛物线y²=2px的焦点F（1，0），且与抛物线相交于A、B两点．
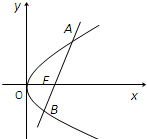
（1）求该抛物线的标准方程和准线方程；
（2）求线段AB的长．

Answer 1

分析：（1）根据焦点可求出p的值，从而求出抛物线的方程，即可得到准线方程；
（2）设A（x₁，y₁），B（x₂，y₂），将直线l的方程与抛物线方程联立消去y，整理得4x²-17x+4=0，得到根与系数的关系，由抛物线的定义可知|AB|=x₁+x₂+p，代入即可求出所求．

解答：解：（1）由焦点F（1，0），得

p

2

=1，解得p=2．…（2分）
所以抛物线的方程为y²=4x，其准线方程为x=-1，…（4分）
（2）设A（x₁，y₁），B（x₂，y₂）．
直线l的方程为y=

4

3

•(x-1)．    …（5分）
与抛物线方程联立，得

y= 4 3 (x-1) y2=4x

，…（7分）
消去y，整理得4x²-17x+4=0，…（9分）
由抛物线的定义可知，|AB|=x1+x2+p=

17

4

+2=

25

4

．
所以，线段AB的长为

25

4

．…（13分）

点评：本题主要考查了抛物线的标准方程，以及过焦点的直线与抛物线相交的弦长等问题，属于中档题．